There is an undirected graph of n nodes. You are given a 2D array edges, where edges[i] = [u_i, v_i, length_i] describes an edge between node u_i and node v_i with a traversal time of length_i units.

Additionally, you are given an array disappear, where disappear[i] denotes the time when the node i disappears from the graph and you won't be able to visit it.

Notice that the graph might be disconnected and might contain multiple edges.

Return the array answer, with answer[i] denoting the minimum units of time required to reach node i from node 0. If node i is unreachable from node 0 then answer[i] is -1.

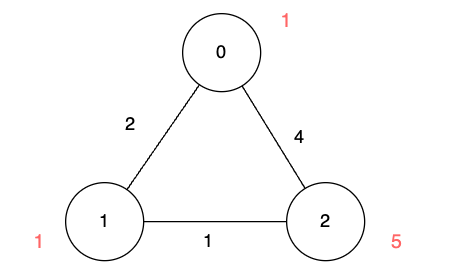
Example 1:

Input: n = 3, edges = [[0,1,2],[1,2,1],[0,2,4]], disappear = [1,1,5]

Output: [0,-1,4]

Explanation:

We are starting our journey from node 0, and our goal is to find the minimum time required to reach each node before it disappears.

For node 0, we don't need any time as it is our starting point.
For node 1, we need at least 2 units of time to traverse edges[0]. Unfortunately, it disappears at that moment, so we won't be able to visit it.
For node 2, we need at least 4 units of time to traverse edges[2].

Example 2:

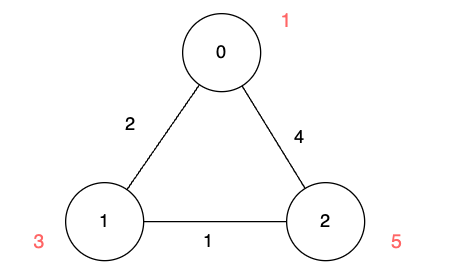
Input: n = 3, edges = [[0,1,2],[1,2,1],[0,2,4]], disappear = [1,3,5]

Output: [0,2,3]

Explanation:

We are starting our journey from node 0, and our goal is to find the minimum time required to reach each node before it disappears.

For node 0, we don't need any time as it is the starting point.
For node 1, we need at least 2 units of time to traverse edges[0].
For node 2, we need at least 3 units of time to traverse edges[0] and edges[1].

Example 3:

Input: n = 2, edges = [[0,1,1]], disappear = [1,1]

Output: [0,-1]

Explanation:

Exactly when we reach node 1, it disappears.

Constraints:

1 <= n <= 5 * 10⁴
0 <= edges.length <= 10⁵
edges[i] == [u_i, v_i, length_i]
0 <= u_i, v_i <= n - 1
1 <= length_i <= 10⁵
disappear.length == n
1 <= disappear[i] <= 10⁵