There is an undirected tree with n nodes labeled from 1 to n, rooted at node 1. The tree is represented by a 2D integer array edges of length n - 1, where edges[i] = [u_i, v_i] indicates that there is an edge between nodes u_i and v_i.

Initially, all edges have a weight of 0. You must assign each edge a weight of either 1 or 2.

The cost of a path between any two nodes u and v is the total weight of all edges in the path connecting them.

You are given a 2D integer array queries. For each queries[i] = [u_i, v_i], determine the number of ways to assign weights to edges in the path such that the cost of the path between u_i and v_i is odd.

Return an array answer, where answer[i] is the number of valid assignments for queries[i].

Since the answer may be large, apply modulo 10⁹ + 7 to each answer[i].

Note: For each query, disregard all edges not in the path between node u_i and v_i.

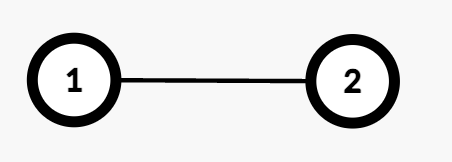
Input: edges = [[1,2]], queries = [[1,1],[1,2]]

Output: [0,1]

Explanation:

Query [1,1]: The path from Node 1 to itself consists of no edges, so the cost is 0. Thus, the number of valid assignments is 0.
Query [1,2]: The path from Node 1 to Node 2 consists of one edge (1 → 2). Assigning weight 1 makes the cost odd, while 2 makes it even. Thus, the number of valid assignments is 1.

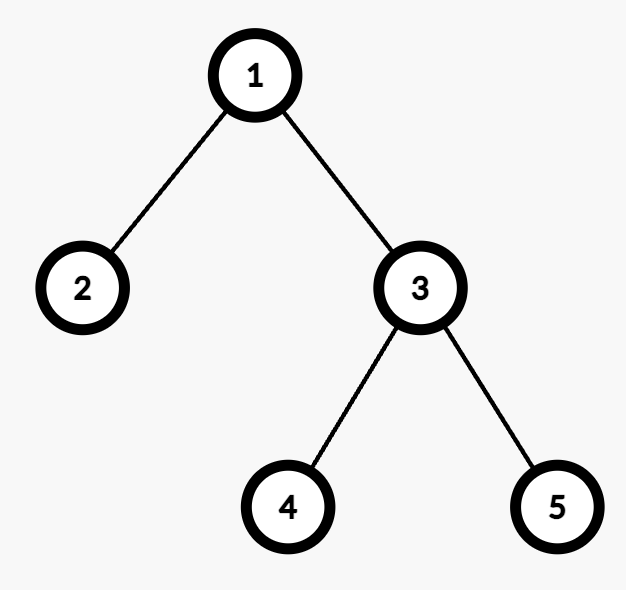
Input: edges = [[1,2],[1,3],[3,4],[3,5]], queries = [[1,4],[3,4],[2,5]]

Output: [2,1,4]

Explanation:

Query [1,4]: The path from Node 1 to Node 4 consists of two edges (1 → 3 and 3 → 4). Assigning weights (1,2) or (2,1) results in an odd cost. Thus, the number of valid assignments is 2.
Query [3,4]: The path from Node 3 to Node 4 consists of one edge (3 → 4). Assigning weight 1 makes the cost odd, while 2 makes it even. Thus, the number of valid assignments is 1.
Query [2,5]: The path from Node 2 to Node 5 consists of three edges (2 → 1, 1 → 3, and 3 → 5). Assigning (1,2,2), (2,1,2), (2,2,1), or (1,1,1) makes the cost odd. Thus, the number of valid assignments is 4.