给你一个包含 n 个节点（编号从 0 到 n - 1）的有向无环图。图由长度为 m 的二维数组 edges 表示，其中 edges[i] = [ui, vi, costi] 表示从节点 ui 到节点 vi 的单向通信，恢复成本为 costi。
一些节点可能处于离线状态。给定一个布尔数组 online，其中 online[i] = true 表示节点 i 在线。节点 0 和 n - 1 始终在线。
从 0 到 n - 1 的路径如果满足以下条件，那么它是 有效 的：
k。对于每条有效路径，其 分数 定义为该路径上的最小边成本。
返回所有有效路径中的 最大 路径分数（即最大 最小 边成本）。如果没有有效路径，则返回 -1。
示例 1:
输入: edges = [[0,1,5],[1,3,10],[0,2,3],[2,3,4]], online = [true,true,true,true], k = 10
输出: 3
解释:
图中有两条从节点 0 到节点 3 的可能路线：
路径 0 → 1 → 3
总成本 = 5 + 10 = 15，超过了 k (15 > 10)，因此此路径无效。
路径 0 → 2 → 3
总成本 = 3 + 4 = 7 <= k，因此此路径有效。
此路径上的最小边成本为 min(3, 4) = 3。
没有其他有效路径。因此，所有有效路径分数中的最大值为 3。
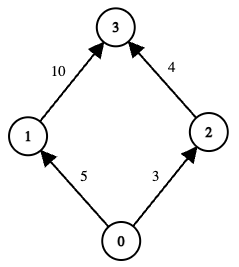
示例 2:
输入: edges = [[0,1,7],[1,4,5],[0,2,6],[2,3,6],[3,4,2],[2,4,6]], online = [true,true,true,false,true], k = 12
输出: 6
解释:
节点 3 离线，因此任何通过 3 的路径都是无效的。
考虑从 0 到 4 的其余路线：
路径 0 → 1 → 4
总成本 = 7 + 5 = 12 <= k，因此此路径有效。
此路径上的最小边成本为 min(7, 5) = 5。
路径 0 → 2 → 3 → 4
节点 3 离线，因此无论成本多少，此路径无效。
路径 0 → 2 → 4
总成本 = 6 + 6 = 12 <= k，因此此路径有效。
此路径上的最小边成本为 min(6, 6) = 6。
在两条有效路径中，它们的分数分别为 5 和 6。因此，答案是 6。
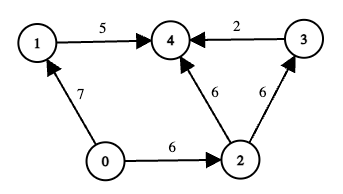
提示:
n == online.length2 <= n <= 5 * 1040 <= m == edges.length <= min(105, n * (n - 1) / 2)edges[i] = [ui, vi, costi]0 <= ui, vi < nui != vi0 <= costi <= 1090 <= k <= 5 * 1013online[i] 是 true 或 false，且 online[0] 和 online[n - 1] 均为 true。