There is an 8 x 8 chessboard containing n pieces (rooks, queens, or bishops). You are given a string array pieces of length n, where pieces[i] describes the type (rook, queen, or bishop) of the ith piece. In addition, you are given a 2D integer array positions also of length n, where positions[i] = [ri, ci] indicates that the ith piece is currently at the 1-based coordinate (ri, ci) on the chessboard.
When making a move for a piece, you choose a destination square that the piece will travel toward and stop on.
(r, c) to the direction of (r+1, c), (r-1, c), (r, c+1), or (r, c-1).(r, c) to the direction of (r+1, c), (r-1, c), (r, c+1), (r, c-1), (r+1, c+1), (r+1, c-1), (r-1, c+1), (r-1, c-1).(r, c) to the direction of (r+1, c+1), (r+1, c-1), (r-1, c+1), (r-1, c-1).You must make a move for every piece on the board simultaneously. A move combination consists of all the moves performed on all the given pieces. Every second, each piece will instantaneously travel one square towards their destination if they are not already at it. All pieces start traveling at the 0th second. A move combination is invalid if, at a given time, two or more pieces occupy the same square.
Return the number of valid move combinations.
Notes:
Example 1:
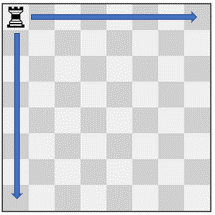
Input: pieces = ["rook"], positions = [[1,1]] Output: 15 Explanation: The image above shows the possible squares the piece can move to.
Example 2:
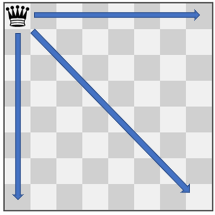
Input: pieces = ["queen"], positions = [[1,1]] Output: 22 Explanation: The image above shows the possible squares the piece can move to.
Example 3:
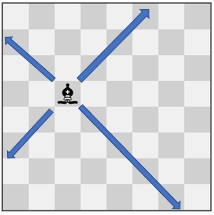
Input: pieces = ["bishop"], positions = [[4,3]] Output: 12 Explanation: The image above shows the possible squares the piece can move to.
Constraints:
n == pieces.length n == positions.length1 <= n <= 4pieces only contains the strings "rook", "queen", and "bishop".1 <= xi, yi <= 8positions[i] is distinct.