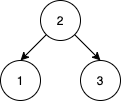
给你一个数组 nums 表示 1 到 n 的一个排列。我们按照元素在 nums 中的顺序依次插入一个初始为空的二叉查找树(BST)。请你统计将 nums 重新排序后,统计满足如下条件的方案数:重排后得到的二叉查找树与 nums 原本数字顺序得到的二叉查找树相同。
比方说,给你 nums = [2,1,3],我们得到一棵 2 为根,1 为左孩子,3 为右孩子的树。数组 [2,3,1] 也能得到相同的 BST,但 [3,2,1] 会得到一棵不同的 BST 。
请你返回重排 nums 后,与原数组 nums 得到相同二叉查找树的方案数。
由于答案可能会很大,请将结果对 10^9 + 7 取余数。
示例 1:

输入:nums = [2,1,3] 输出:1 解释:我们将 nums 重排, [2,3,1] 能得到相同的 BST 。没有其他得到相同 BST 的方案了。
示例 2:
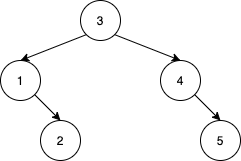
输入:nums = [3,4,5,1,2] 输出:5 解释:下面 5 个数组会得到相同的 BST: [3,1,2,4,5] [3,1,4,2,5] [3,1,4,5,2] [3,4,1,2,5] [3,4,1,5,2]
示例 3:
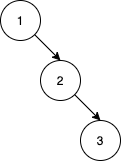
输入:nums = [1,2,3] 输出:0 解释:没有别的排列顺序能得到相同的 BST 。
示例 4:
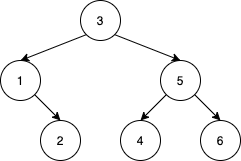
输入:nums = [3,1,2,5,4,6] 输出:19
示例 5:
输入:nums = [9,4,2,1,3,6,5,7,8,14,11,10,12,13,16,15,17,18] 输出:216212978 解释:得到相同 BST 的方案数是 3216212999。将它对 10^9 + 7 取余后得到 216212978。
提示:
1 <= nums.length <= 10001 <= nums[i] <= nums.lengthnums 中所有数 互不相同 。