<p>给你一个下标从 <strong>1</strong> 开始、大小为 <code>m x n</code> 的整数矩阵 <code>mat</code>，你可以选择任一单元格作为 <strong>起始单元格</strong> 。</p>

<p>从起始单元格出发，你可以移动到 <strong>同一行或同一列</strong> 中的任何其他单元格，但前提是目标单元格的值<strong> 严格大于 </strong>当前单元格的值。</p>

<p>你可以多次重复这一过程，从一个单元格移动到另一个单元格，直到无法再进行任何移动。</p>

<p>请你找出从某个单元开始访问矩阵所能访问的 <strong>单元格的最大数量</strong> 。</p>

<p>返回一个表示可访问单元格最大数量的整数。</p>

<p>&nbsp;</p>

<p><strong>示例 1：</strong></p>

<p><strong><img alt="" src="https://assets.leetcode.com/uploads/2023/04/23/diag1drawio.png" style="width: 200px; height: 176px;"></strong></p>

<pre><strong>输入：</strong>mat = [[3,1],[3,4]]
<strong>输出：</strong>2
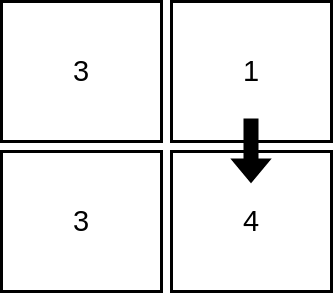
<strong>解释：</strong>上图展示了从第 1 行、第 2 列的单元格开始，可以访问 2 个单元格。可以证明，无论从哪个单元格开始，最多只能访问 2 个单元格，因此答案是 2 。 
</pre>

<p><strong>示例 2：</strong></p>

<p><strong><img alt="" src="https://assets.leetcode.com/uploads/2023/04/23/diag3drawio.png" style="width: 200px; height: 176px;"></strong></p>

<pre><strong>输入：</strong>mat = [[1,1],[1,1]]
<strong>输出：</strong>1
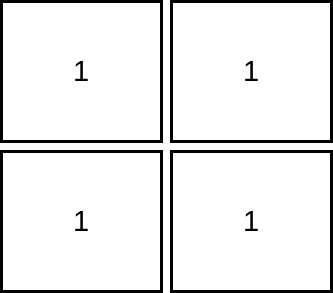
<strong>解释：</strong>由于目标单元格必须严格大于当前单元格，在本示例中只能访问 1 个单元格。 
</pre>

<p><strong>示例 3：</strong></p>

<p><strong><img alt="" src="https://assets.leetcode.com/uploads/2023/04/23/diag4drawio.png" style="width: 350px; height: 250px;"></strong></p>

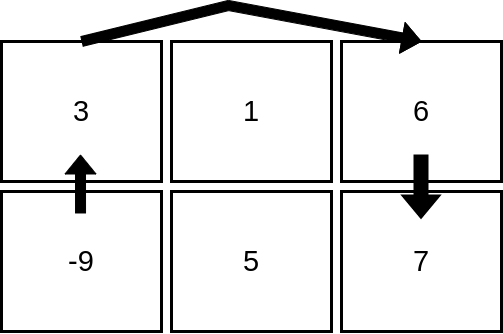
<pre><strong>输入：</strong>mat = [[3,1,6],[-9,5,7]]
<strong>输出：</strong>4
<strong>解释：</strong>上图展示了从第 2 行、第 1 列的单元格开始，可以访问 4 个单元格。可以证明，无论从哪个单元格开始，最多只能访问 4 个单元格，因此答案是 4 。  
</pre>

<p>&nbsp;</p>

<p><strong>提示：</strong></p>

<ul>
	<li><code>m == mat.length&nbsp;</code></li>
	<li><code>n == mat[i].length&nbsp;</code></li>
	<li><code>1 &lt;= m, n &lt;= 10<sup>5</sup></code></li>
	<li><code>1 &lt;= m * n &lt;= 10<sup>5</sup></code></li>
	<li><code>-10<sup>5</sup>&nbsp;&lt;= mat[i][j] &lt;= 10<sup>5</sup></code></li>
</ul>