There are n teams numbered from 0 to n - 1 in a tournament; each team is also a node in a DAG.
You are given the integer n and a 0-indexed 2D integer array edges of length m representing the DAG, where edges[i] = [ui, vi] indicates that there is a directed edge from team ui to team vi in the graph.
A directed edge from a to b in the graph means that team a is stronger than team b and team b is weaker than team a.
Team a will be the champion of the tournament if there is no team b that is stronger than team a.
Return the team that will be the champion of the tournament if there is a unique champion, otherwise, return -1.
Notes
a1, a2, ..., an, an+1 such that node a1 is the same node as node an+1, the nodes a1, a2, ..., an are distinct, and there is a directed edge from the node ai to node ai+1 for every i in the range [1, n].
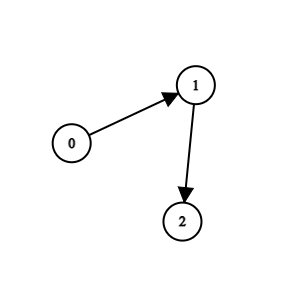
Example 1:

Input: n = 3, edges = [[0,1],[1,2]] Output: 0 Explanation: Team 1 is weaker than team 0. Team 2 is weaker than team 1. So the champion is team 0.
Example 2:
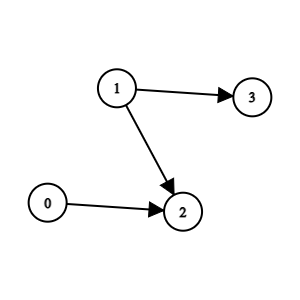
Input: n = 4, edges = [[0,2],[1,3],[1,2]] Output: -1 Explanation: Team 2 is weaker than team 0 and team 1. Team 3 is weaker than team 1. But team 1 and team 0 are not weaker than any other teams. So the answer is -1.
Constraints:
1 <= n <= 100m == edges.length0 <= m <= n * (n - 1) / 2edges[i].length == 20 <= edge[i][j] <= n - 1edges[i][0] != edges[i][1]a is stronger than team b, team b is not stronger than team a.a is stronger than team b and team b is stronger than team c, then team a is stronger than team c.