You are given an integer n and a directed graph with n nodes labeled from 0 to n - 1. This is represented by a 2D array edges, where edges[i] = [u_i, v_i, start_i, end_i] indicates an edge from node u_i to v_i that can only be used at any integer time t such that start_i <= t <= end_i.

You start at node 0 at time 0.

In one unit of time, you can either:

Wait at your current node without moving, or
Travel along an outgoing edge from your current node if the current time t satisfies start_i <= t <= end_i.

Return the minimum time required to reach node n - 1. If it is impossible, return -1.

Example 1:

Input: n = 3, edges = [[0,1,0,1],[1,2,2,5]]

Output: 3

Explanation:

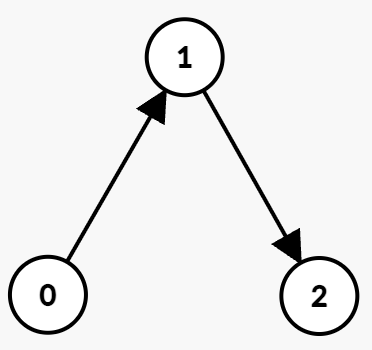
The optimal path is:

At time t = 0, take the edge (0 → 1) which is available from 0 to 1. You arrive at node 1 at time t = 1, then wait until t = 2.
At time t = 2, take the edge (1 → 2) which is available from 2 to 5. You arrive at node 2 at time 3.

Hence, the minimum time to reach node 2 is 3.

Example 2:

Input: n = 4, edges = [[0,1,0,3],[1,3,7,8],[0,2,1,5],[2,3,4,7]]

Output: 5

Explanation:

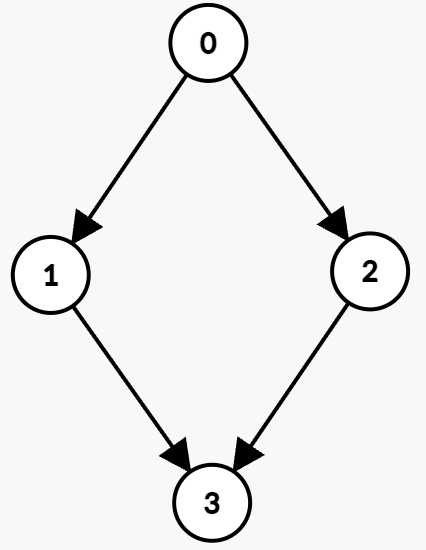
The optimal path is:

Wait at node 0 until time t = 1, then take the edge (0 → 2) which is available from 1 to 5. You arrive at node 2 at t = 2.
Wait at node 2 until time t = 4, then take the edge (2 → 3) which is available from 4 to 7. You arrive at node 3 at t = 5.

Hence, the minimum time to reach node 3 is 5.

Example 3:

Input: n = 3, edges = [[1,0,1,3],[1,2,3,5]]

Output: -1

Explanation:

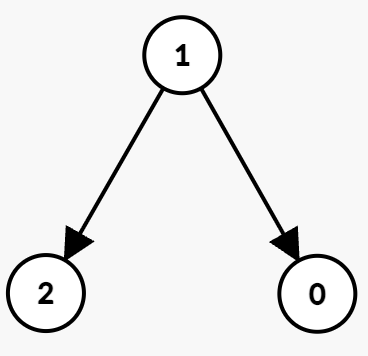
Since there is no outgoing edge from node 0, it is impossible to reach node 2. Hence, the output is -1.

Constraints:

1 <= n <= 10⁵
0 <= edges.length <= 10⁵
edges[i] == [u_i, v_i, start_i, end_i]
0 <= u_i, v_i <= n - 1
u_i != v_i
0 <= start_i <= end_i <= 10⁹