输入: n = 5, edges = [[0,1,4],[1,2,3],[1,3,2],[3,4,6]], k = 2
输出: 4
解释:
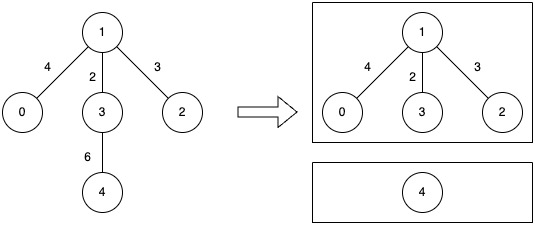
- 移除节点 3 和节点 4 之间的边(权值为 6)。
- 最终的连通分量成本分别为 0 和 4,因此最大代价为 4。
给你一个无向连通图,包含 n 个节点,节点编号从 0 到 n - 1,以及一个二维整数数组 edges,其中 edges[i] = [ui, vi, wi] 表示一条连接节点 ui 和节点 vi 的无向边,边权为 wi,另有一个整数 k。
你可以从图中移除任意数量的边,使得最终的图中 最多 只包含 k 个连通分量。
连通分量的 成本 定义为该分量中边权的 最大值 。如果一个连通分量没有边,则其代价为 0。
请返回在移除这些边之后,在所有连通分量之中的 最大成本 的 最小可能值 。
示例 1:
输入: n = 5, edges = [[0,1,4],[1,2,3],[1,3,2],[3,4,6]], k = 2
输出: 4
解释:

示例 2:
输入: n = 4, edges = [[0,1,5],[1,2,5],[2,3,5]], k = 1
输出: 5
解释:

k = 1),图必须保持完全连通。
提示:
1 <= n <= 5 * 1040 <= edges.length <= 105edges[i].length == 30 <= ui, vi < n1 <= wi <= 1061 <= k <= n