给你一个 值互不相同 的二叉树的根节点 root 。

在一步操作中，你可以选择 同一层 上任意两个节点，交换这两个节点的值。

返回每一层按 严格递增顺序 排序所需的最少操作数目。

节点的 层数 是该节点和根节点之间的路径的边数。

示例 1 ：

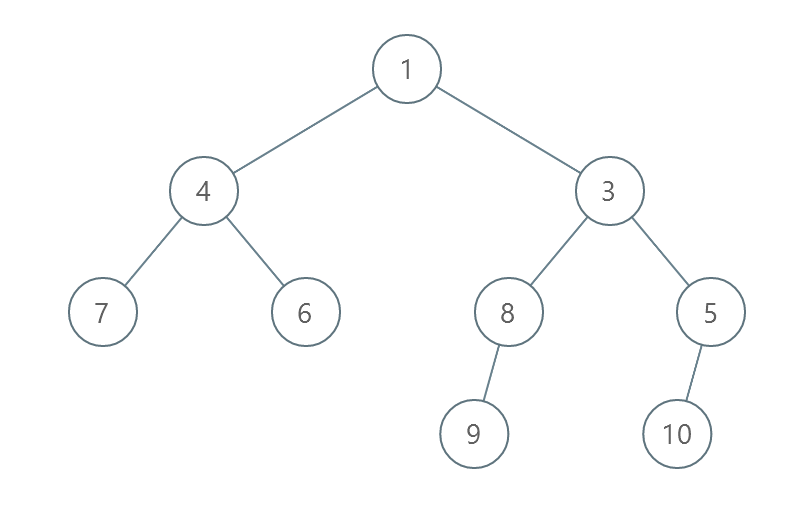
输入：root = [1,4,3,7,6,8,5,null,null,null,null,9,null,10]
输出：3
解释：
- 交换 4 和 3 。第 2 层变为 [3,4] 。
- 交换 7 和 5 。第 3 层变为 [5,6,8,7] 。
- 交换 8 和 7 。第 3 层变为 [5,6,7,8] 。
共计用了 3 步操作，所以返回 3 。
可以证明 3 是需要的最少操作数目。

示例 2 ：

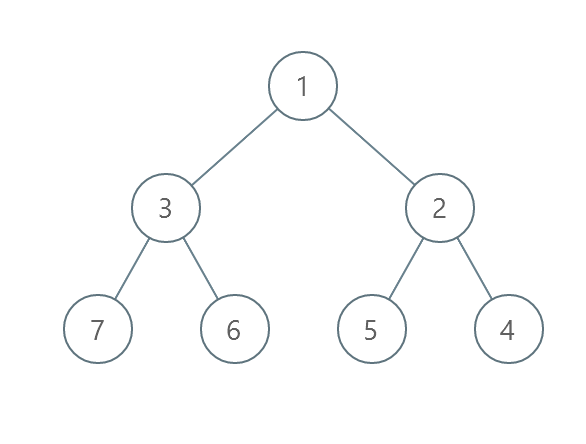
输入：root = [1,3,2,7,6,5,4]
输出：3
解释：
- 交换 3 和 2 。第 2 层变为 [2,3] 。 
- 交换 7 和 4 。第 3 层变为 [4,6,5,7] 。 
- 交换 6 和 5 。第 3 层变为 [4,5,6,7] 。
共计用了 3 步操作，所以返回 3 。 
可以证明 3 是需要的最少操作数目。

示例 3 ：

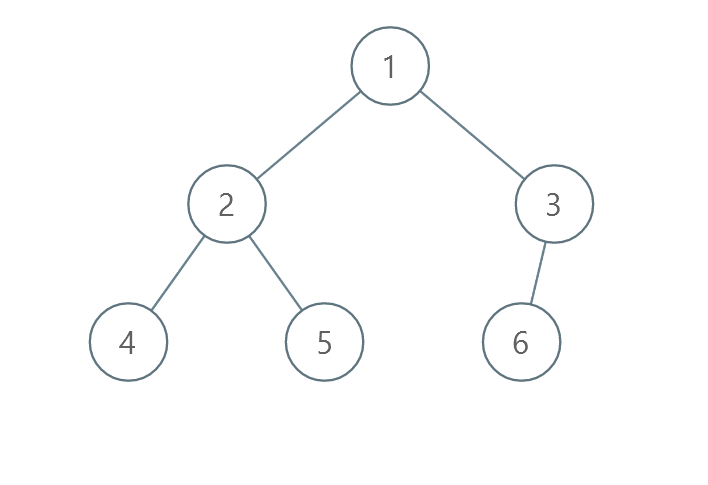
输入：root = [1,2,3,4,5,6]
输出：0
解释：每一层已经按递增顺序排序，所以返回 0 。

提示：

• 树中节点的数目在范围 [1, 105] 。
• 1 <= Node.val <= 105
• 树中的所有值 互不相同 。