给你一个下标从 0 开始、大小为 n x n 的二维矩阵 grid ,其中 (r, c) 表示:
grid[r][c] = 1 ,则表示一个存在小偷的单元格grid[r][c] = 0 ,则表示一个空单元格你最开始位于单元格 (0, 0) 。在一步移动中,你可以移动到矩阵中的任一相邻单元格,包括存在小偷的单元格。
矩阵中路径的 安全系数 定义为:从路径中任一单元格到矩阵中任一小偷所在单元格的 最小 曼哈顿距离。
返回所有通向单元格 (n - 1, n - 1) 的路径中的 最大安全系数 。
单元格 (r, c) 的某个 相邻 单元格,是指在矩阵中存在的 (r, c + 1)、(r, c - 1)、(r + 1, c) 和 (r - 1, c) 之一。
两个单元格 (a, b) 和 (x, y) 之间的 曼哈顿距离 等于 | a - x | + | b - y | ,其中 |val| 表示 val 的绝对值。
示例 1:
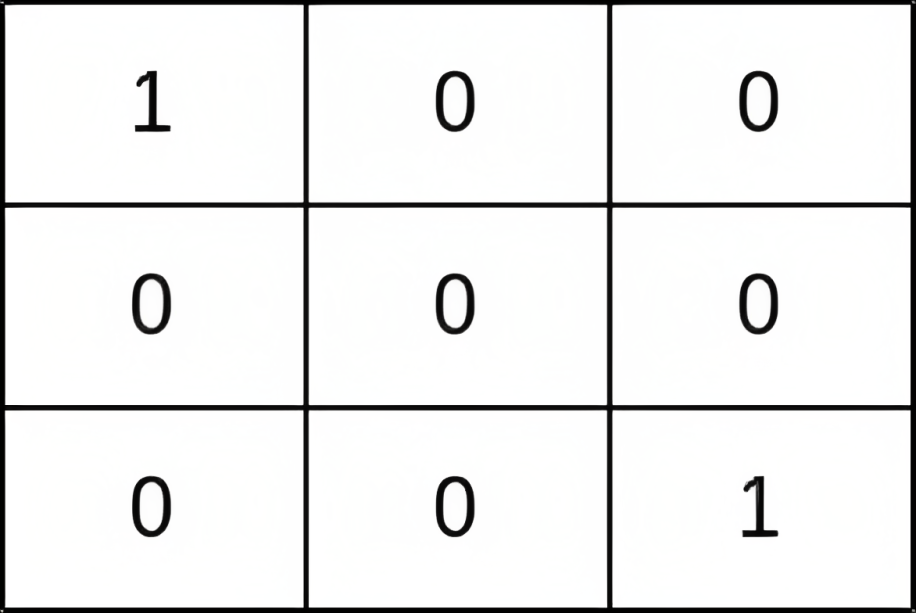
输入:grid = [[1,0,0],[0,0,0],[0,0,1]] 输出:0 解释:从 (0, 0) 到 (n - 1, n - 1) 的每条路径都经过存在小偷的单元格 (0, 0) 和 (n - 1, n - 1) 。
示例 2:
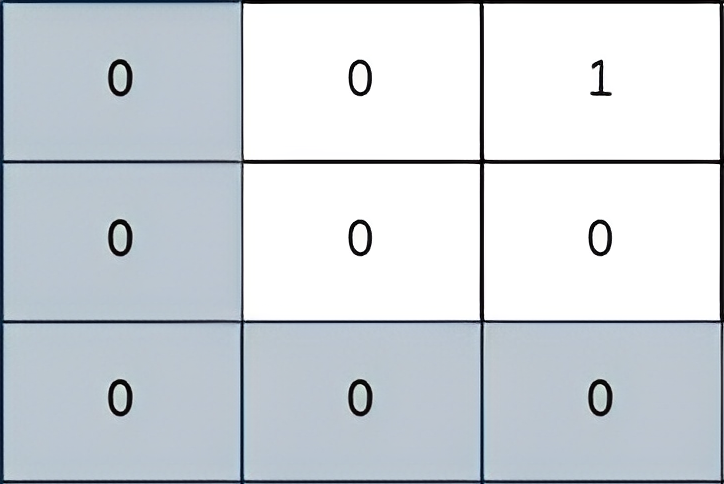
输入:grid = [[0,0,1],[0,0,0],[0,0,0]] 输出:2 解释: 上图所示路径的安全系数为 2: - 该路径上距离小偷所在单元格(0,2)最近的单元格是(0,0)。它们之间的曼哈顿距离为 | 0 - 0 | + | 0 - 2 | = 2 。 可以证明,不存在安全系数更高的其他路径。
示例 3:
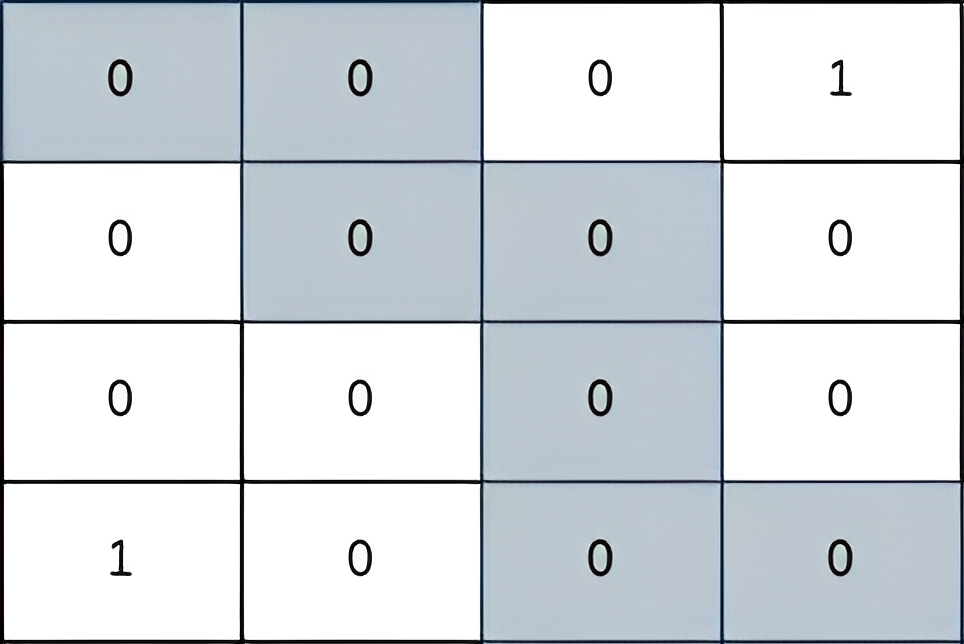
输入:grid = [[0,0,0,1],[0,0,0,0],[0,0,0,0],[1,0,0,0]] 输出:2 解释: 上图所示路径的安全系数为 2: - 该路径上距离小偷所在单元格(0,3)最近的单元格是(1,2)。它们之间的曼哈顿距离为 | 0 - 1 | + | 3 - 2 | = 2 。 - 该路径上距离小偷所在单元格(3,0)最近的单元格是(3,2)。它们之间的曼哈顿距离为 | 3 - 3 | + | 0 - 2 | = 2 。 可以证明,不存在安全系数更高的其他路径。
提示:
1 <= grid.length == n <= 400grid[i].length == ngrid[i][j] 为 0 或 1grid 至少存在一个小偷