给你一个下标从 0 开始的二维整数数组 grid ，它的大小为 m x n ，表示一个商店中物品的分布图。数组中的整数含义为：

从一个格子走到上下左右相邻格子花费 1 步。

同时给你一个整数数组 pricing 和 start ，其中 pricing = [low, high] 且 start = [row, col] ，表示你开始位置为 (row, col) ，同时你只对物品价格在 闭区间 [low, high] 之内的物品感兴趣。同时给你一个整数 k 。

你想知道给定范围 内 且 排名最高 的 k 件物品的 位置 。排名按照优先级从高到低的以下规则制定：

  1. 距离：定义为从 start 到一件物品的最短路径需要的步数（较近 距离的排名更高）。
  2. 价格：较低 价格的物品有更高优先级，但只考虑在给定范围之内的价格。
  3. 行坐标：较小 行坐标的有更高优先级。
  4. 列坐标：较小 列坐标的有更高优先级。

请你返回给定价格内排名最高的 k 件物品的坐标，将它们按照排名排序后返回。如果给定价格内少于 k 件物品，那么请将它们的坐标 全部 返回。

 

示例 1：

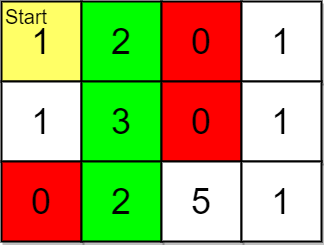
输入：grid = [[1,2,0,1],[1,3,0,1],[0,2,5,1]], pricing = [2,5], start = [0,0], k = 3
输出：[[0,1],[1,1],[2,1]]
解释：起点为 (0,0) 。
价格范围为 [2,5] ，我们可以选择的物品坐标为 (0,1)，(1,1)，(2,1) 和 (2,2) 。
这些物品的排名为：
- (0,1) 距离为 1
- (1,1) 距离为 2
- (2,1) 距离为 3
- (2,2) 距离为 4
所以，给定价格范围内排名最高的 3 件物品的坐标为 (0,1)，(1,1) 和 (2,1) 。

示例 2：

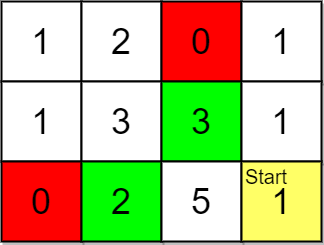
输入：grid = [[1,2,0,1],[1,3,3,1],[0,2,5,1]], pricing = [2,3], start = [2,3], k = 2
输出：[[2,1],[1,2]]
解释：起点为 (2,3) 。
价格范围为 [2,3] ，我们可以选择的物品坐标为 (0,1)，(1,1)，(1,2) 和 (2,1) 。
这些物品的排名为： 
- (2,1) 距离为 2 ，价格为 2
- (1,2) 距离为 2 ，价格为 3
- (1,1) 距离为 3
- (0,1) 距离为 4
所以，给定价格范围内排名最高的 2 件物品的坐标为 (2,1) 和 (1,2) 。

示例 3：

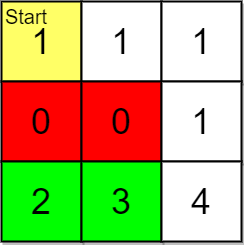
输入：grid = [[1,1,1],[0,0,1],[2,3,4]], pricing = [2,3], start = [0,0], k = 3
输出：[[2,1],[2,0]]
解释：起点为 (0,0) 。
价格范围为 [2,3] ，我们可以选择的物品坐标为 (2,0) 和 (2,1) 。
这些物品的排名为：
- (2,1) 距离为 5
- (2,0) 距离为 6
所以，给定价格范围内排名最高的 2 件物品的坐标为 (2,1) 和 (2,0) 。
注意，k = 3 但给定价格范围内只有 2 件物品。

 

提示：