输入:grid = [[0,0,0,0,0],[0,0,3,0,0],[0,1,0,0,0],[5,0,0,3,0],[0,0,0,0,2]]
输出:11
解释:
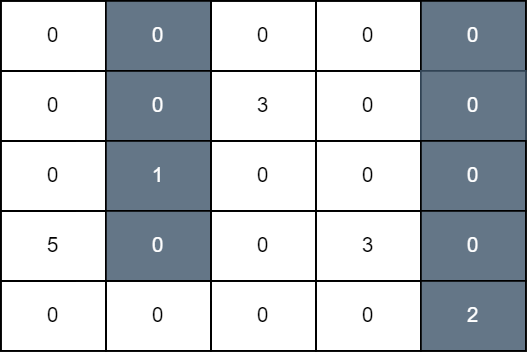
第一次操作中,我们将第 1 列中,最上面的格子到第 3 行的格子染成黑色。第二次操作中,我们将第 4 列中,最上面的格子到最后一行的格子染成黑色。最后网格图总分为 grid[3][0] + grid[1][2] + grid[3][3] 等于 11 。
给你一个大小为 n x n 的二维矩阵 grid ,一开始所有格子都是白色的。一次操作中,你可以选择任意下标为 (i, j) 的格子,并将第 j 列中从最上面到第 i 行所有格子改成黑色。
如果格子 (i, j) 为白色,且左边或者右边的格子至少一个格子为黑色,那么我们将 grid[i][j] 加到最后网格图的总分中去。
请你返回执行任意次操作以后,最终网格图的 最大 总分数。
示例 1:
输入:grid = [[0,0,0,0,0],[0,0,3,0,0],[0,1,0,0,0],[5,0,0,3,0],[0,0,0,0,2]]
输出:11
解释:

第一次操作中,我们将第 1 列中,最上面的格子到第 3 行的格子染成黑色。第二次操作中,我们将第 4 列中,最上面的格子到最后一行的格子染成黑色。最后网格图总分为 grid[3][0] + grid[1][2] + grid[3][3] 等于 11 。
示例 2:
输入:grid = [[10,9,0,0,15],[7,1,0,8,0],[5,20,0,11,0],[0,0,0,1,2],[8,12,1,10,3]]
输出:94
解释:
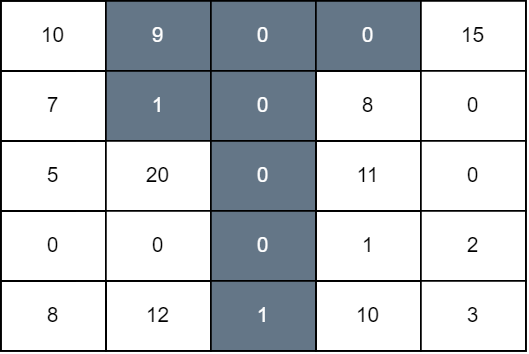
我们对第 1 ,2 ,3 列分别从上往下染黑色到第 1 ,4, 0 行。最后网格图总分为 grid[0][0] + grid[1][0] + grid[2][1] + grid[4][1] + grid[1][3] + grid[2][3] + grid[3][3] + grid[4][3] + grid[0][4] 等于 94 。
提示:
1 <= n == grid.length <= 100n == grid[i].length0 <= grid[i][j] <= 109