给你一个 n 个节点的无向带权图,节点编号为 0 到 n - 1 。图中总共有 m 条边,用二维数组 edges 表示,其中 edges[i] = [ai, bi, wi] 表示节点 ai 和 bi 之间有一条边权为 wi 的边。
对于节点 0 为出发点,节点 n - 1 为结束点的所有最短路,你需要返回一个长度为 m 的 boolean 数组 answer ,如果 edges[i] 至少 在其中一条最短路上,那么 answer[i] 为 true ,否则 answer[i] 为 false 。
请你返回数组 answer 。
注意,图可能不连通。
示例 1:

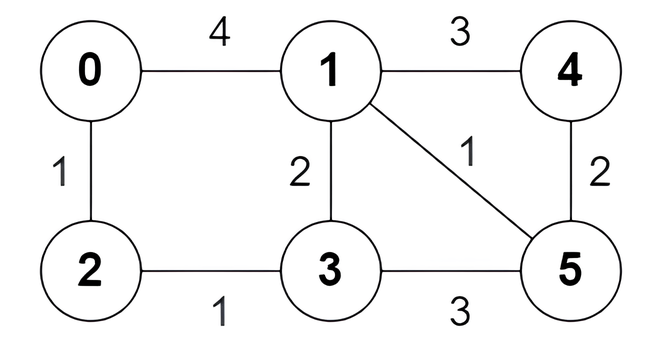
输入:n = 6, edges = [[0,1,4],[0,2,1],[1,3,2],[1,4,3],[1,5,1],[2,3,1],[3,5,3],[4,5,2]]
输出:[true,true,true,false,true,true,true,false]
解释:
以下为节点 0 出发到达节点 5 的 所有 最短路:
0 -> 1 -> 5 :边权和为 4 + 1 = 5 。0 -> 2 -> 3 -> 5 :边权和为 1 + 1 + 3 = 5 。0 -> 2 -> 3 -> 1 -> 5 :边权和为 1 + 1 + 2 + 1 = 5 。示例 2:
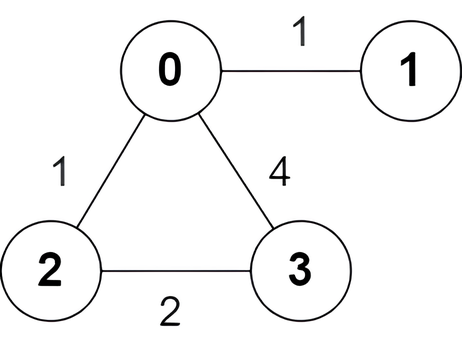
输入:n = 4, edges = [[2,0,1],[0,1,1],[0,3,4],[3,2,2]]
输出:[true,false,false,true]
解释:
只有一条从节点 0 出发到达节点 3 的最短路 0 -> 2 -> 3 ,边权和为 1 + 2 = 3 。
提示:
2 <= n <= 5 * 104m == edges.length1 <= m <= min(5 * 104, n * (n - 1) / 2)0 <= ai, bi < nai != bi1 <= wi <= 105