You are given a positive integer k. You are also given:
rowConditions of size n where rowConditions[i] = [abovei, belowi], andcolConditions of size m where colConditions[i] = [lefti, righti].The two arrays contain integers from 1 to k.
You have to build a k x k matrix that contains each of the numbers from 1 to k exactly once. The remaining cells should have the value 0.
The matrix should also satisfy the following conditions:
abovei should appear in a row that is strictly above the row at which the number belowi appears for all i from 0 to n - 1.lefti should appear in a column that is strictly left of the column at which the number righti appears for all i from 0 to m - 1.Return any matrix that satisfies the conditions. If no answer exists, return an empty matrix.
Example 1:
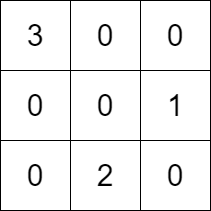
Input: k = 3, rowConditions = [[1,2],[3,2]], colConditions = [[2,1],[3,2]] Output: [[3,0,0],[0,0,1],[0,2,0]] Explanation: The diagram above shows a valid example of a matrix that satisfies all the conditions. The row conditions are the following: - Number 1 is in row 1, and number 2 is in row 2, so 1 is above 2 in the matrix. - Number 3 is in row 0, and number 2 is in row 2, so 3 is above 2 in the matrix. The column conditions are the following: - Number 2 is in column 1, and number 1 is in column 2, so 2 is left of 1 in the matrix. - Number 3 is in column 0, and number 2 is in column 1, so 3 is left of 2 in the matrix. Note that there may be multiple correct answers.
Example 2:
Input: k = 3, rowConditions = [[1,2],[2,3],[3,1],[2,3]], colConditions = [[2,1]] Output: [] Explanation: From the first two conditions, 3 has to be below 1 but the third conditions needs 3 to be above 1 to be satisfied. No matrix can satisfy all the conditions, so we return the empty matrix.
Constraints:
2 <= k <= 4001 <= rowConditions.length, colConditions.length <= 104rowConditions[i].length == colConditions[i].length == 21 <= abovei, belowi, lefti, righti <= kabovei != belowilefti != righti