You are given an integer n, representing the number of employees in a company. Each employee is assigned a unique ID from 1 to n, and employee 1 is the CEO. You are given two 1-based integer arrays, present and future, each of length n, where:

present[i] represents the current price at which the i^th employee can buy a stock today.
future[i] represents the expected price at which the i^th employee can sell the stock tomorrow.

The company's hierarchy is represented by a 2D integer array hierarchy, where hierarchy[i] = [u_i, v_i] means that employee u_i is the direct boss of employee v_i.

Additionally, you have an integer budget representing the total funds available for investment.

However, the company has a discount policy: if an employee's direct boss purchases their own stock, then the employee can buy their stock at half the original price (floor(present[v] / 2)).

Return the maximum profit that can be achieved without exceeding the given budget.

Note:

You may buy each stock at most once.
You cannot use any profit earned from future stock prices to fund additional investments and must buy only from budget.

Example 1:

Input: n = 2, present = [1,2], future = [4,3], hierarchy = [[1,2]], budget = 3

Output: 5

Explanation:

Employee 1 buys the stock at price 1 and earns a profit of 4 - 1 = 3.
Since Employee 1 is the direct boss of Employee 2, Employee 2 gets a discounted price of floor(2 / 2) = 1.
Employee 2 buys the stock at price 1 and earns a profit of 3 - 1 = 2.
The total buying cost is 1 + 1 = 2 <= budget. Thus, the maximum total profit achieved is 3 + 2 = 5.

Example 2:

Input: n = 2, present = [3,4], future = [5,8], hierarchy = [[1,2]], budget = 4

Output: 4

Explanation:

Employee 2 buys the stock at price 4 and earns a profit of 8 - 4 = 4.
Since both employees cannot buy together, the maximum profit is 4.

Example 3:

Input: n = 3, present = [4,6,8], future = [7,9,11], hierarchy = [[1,2],[1,3]], budget = 10

Output: 10

Explanation:

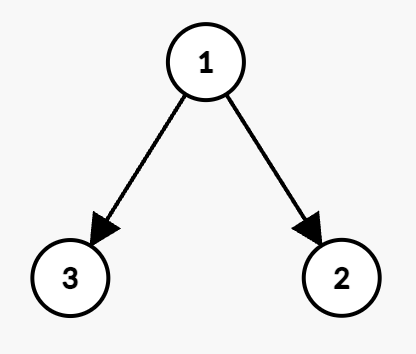
Employee 1 buys the stock at price 4 and earns a profit of 7 - 4 = 3.
Employee 3 would get a discounted price of floor(8 / 2) = 4 and earns a profit of 11 - 4 = 7.
Employee 1 and Employee 3 buy their stocks at a total cost of 4 + 4 = 8 <= budget. Thus, the maximum total profit achieved is 3 + 7 = 10.

Example 4:

Input: n = 3, present = [5,2,3], future = [8,5,6], hierarchy = [[1,2],[2,3]], budget = 7

Output: 12

Explanation:

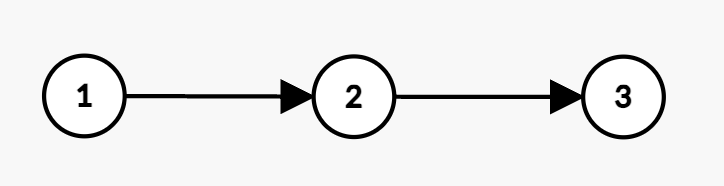
Employee 1 buys the stock at price 5 and earns a profit of 8 - 5 = 3.
Employee 2 would get a discounted price of floor(2 / 2) = 1 and earns a profit of 5 - 1 = 4.
Employee 3 would get a discounted price of floor(3 / 2) = 1 and earns a profit of 6 - 1 = 5.
The total cost becomes 5 + 1 + 1 = 7 <= budget. Thus, the maximum total profit achieved is 3 + 4 + 5 = 12.

Constraints:

1 <= n <= 160
present.length, future.length == n
1 <= present[i], future[i] <= 50
hierarchy.length == n - 1
hierarchy[i] == [u_i, v_i]
1 <= u_i, v_i <= n
u_i != v_i
1 <= budget <= 160
There are no duplicate edges.
Employee 1 is the direct or indirect boss of every employee.
The input graph hierarchy is guaranteed to have no cycles.