You are given three integers m, n, and k.
There is a rectangular grid of size m × n containing k identical pieces. Return the sum of Manhattan distances between every pair of pieces over all valid arrangements of pieces.
A valid arrangement is a placement of all k pieces on the grid with at most one piece per cell.
Since the answer may be very large, return it modulo 109 + 7.
The Manhattan Distance between two cells (xi, yi) and (xj, yj) is |xi - xj| + |yi - yj|.
Example 1:
Input: m = 2, n = 2, k = 2
Output: 8
Explanation:
The valid arrangements of pieces on the board are:

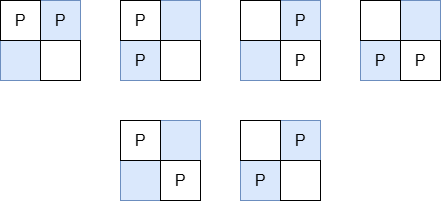
- In the first 4 arrangements, the Manhattan distance between the two pieces is 1.
- In the last 2 arrangements, the Manhattan distance between the two pieces is 2.
Thus, the total Manhattan distance across all valid arrangements is 1 + 1 + 1 + 1 + 2 + 2 = 8.
Example 2:
Input: m = 1, n = 4, k = 3
Output: 20
Explanation:
The valid arrangements of pieces on the board are:

- The first and last arrangements have a total Manhattan distance of
1 + 1 + 2 = 4.
- The middle two arrangements have a total Manhattan distance of
1 + 2 + 3 = 6.
The total Manhattan distance between all pairs of pieces across all arrangements is 4 + 6 + 6 + 4 = 20.
Constraints:
1 <= m, n <= 1052 <= m * n <= 1052 <= k <= m * n


