给你一个 n 个节点的 无向图 ,节点编号为 0 到 n - 1 。
给你一个下标从 0 开始的整数数组 scores ,其中 scores[i] 是第 i 个节点的分数。同时给你一个二维整数数组 edges ,其中 edges[i] = [ai, bi] ,表示节点 ai 和 bi 之间有一条 无向 边。
一个合法的节点序列如果满足以下条件,我们称它是 合法的 :
节点序列的分数定义为序列中节点分数之 和 。
请你返回一个长度为 4 的合法节点序列的最大分数。如果不存在这样的序列,请你返回 -1 。
示例 1:

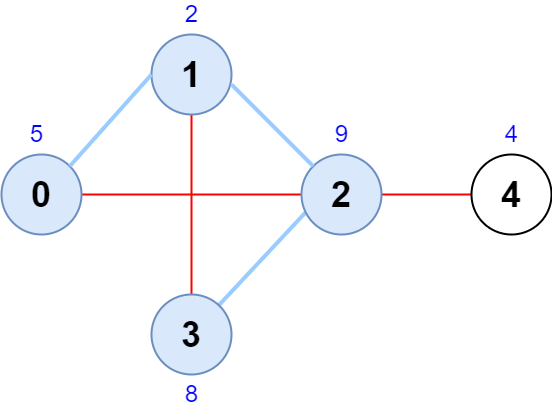
输入:scores = [5,2,9,8,4], edges = [[0,1],[1,2],[2,3],[0,2],[1,3],[2,4]] 输出:24 解释:上图为输入的图,节点序列为 [0,1,2,3] 。 节点序列的分数为 5 + 2 + 9 + 8 = 24 。 观察可知,没有其他节点序列得分和超过 24 。 注意节点序列 [3,1,2,0] 和 [1,0,2,3] 也是合法的,且分数为 24 。 序列 [0,3,2,4] 不是合法的,因为没有边连接节点 0 和 3 。
示例 2:
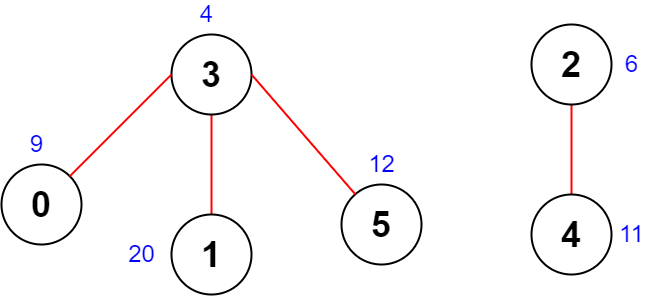
输入:scores = [9,20,6,4,11,12], edges = [[0,3],[5,3],[2,4],[1,3]] 输出:-1 解释:上图为输入的图。 没有长度为 4 的合法序列,所以我们返回 -1 。
提示:
n == scores.length4 <= n <= 5 * 1041 <= scores[i] <= 1080 <= edges.length <= 5 * 104edges[i].length == 20 <= ai, bi <= n - 1ai != bi