输入: edges = [[0,1,4],[0,2,2],[2,3,12],[2,4,6]], k = 2
输出: 22
解释:
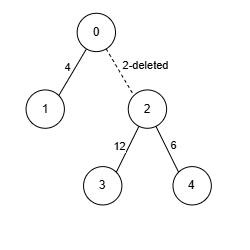
- 节点 2 与其他 3 个节点相连。我们移除边
[0, 2, 2],确保没有节点与超过k = 2个节点相连。 - 权重之和为 22,无法获得更大的和。因此,答案是 22。
存在一棵具有 n 个节点的无向树,节点编号为 0 到 n - 1。给你一个长度为 n - 1 的二维整数数组 edges,其中 edges[i] = [ui, vi, wi] 表示在树中节点 ui 和 vi 之间有一条权重为 wi 的边。
你的任务是移除零条或多条边,使得:
k 个其他节点有边直接相连,其中 k 是给定的输入。返回在进行必要的移除后,剩余边的权重的 最大 可能和。
示例 1:
输入: edges = [[0,1,4],[0,2,2],[2,3,12],[2,4,6]], k = 2
输出: 22
解释:

[0, 2, 2],确保没有节点与超过 k = 2 个节点相连。示例 2:
输入: edges = [[0,1,5],[1,2,10],[0,3,15],[3,4,20],[3,5,5],[0,6,10]], k = 3
输出: 65
解释:
k = 3 个节点相连,我们不移除任何边。
提示:
2 <= n <= 1051 <= k <= n - 1edges.length == n - 1edges[i].length == 30 <= edges[i][0] <= n - 10 <= edges[i][1] <= n - 11 <= edges[i][2] <= 106edges 形成一棵有效的树。