有一个大型的 (m - 1) x (n - 1) 矩形田地,其两个对角分别是 (1, 1) 和 (m, n) ,田地内部有一些水平栅栏和垂直栅栏,分别由数组 hFences 和 vFences 给出。
水平栅栏为坐标 (hFences[i], 1) 到 (hFences[i], n),垂直栅栏为坐标 (1, vFences[i]) 到 (m, vFences[i]) 。
返回通过 移除 一些栅栏(可能不移除)所能形成的最大面积的 正方形 田地的面积,或者如果无法形成正方形田地则返回 -1。
由于答案可能很大,所以请返回结果对 109 + 7 取余 后的值。
注意:田地外围两个水平栅栏(坐标 (1, 1) 到 (1, n) 和坐标 (m, 1) 到 (m, n) )以及两个垂直栅栏(坐标 (1, 1) 到 (m, 1) 和坐标 (1, n) 到 (m, n) )所包围。这些栅栏 不能 被移除。
示例 1:

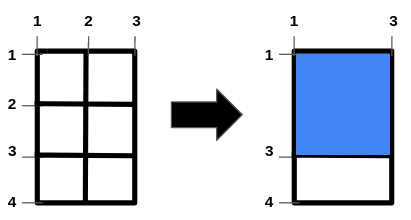
输入:m = 4, n = 3, hFences = [2,3], vFences = [2] 输出:4 解释:移除位于 2 的水平栅栏和位于 2 的垂直栅栏将得到一个面积为 4 的正方形田地。
示例 2:

输入:m = 6, n = 7, hFences = [2], vFences = [4] 输出:-1 解释:可以证明无法通过移除栅栏形成正方形田地。
提示:
3 <= m, n <= 1091 <= hFences.length, vFences.length <= 6001 < hFences[i] < m1 < vFences[i] < nhFences 和 vFences 中的元素是唯一的。