给你一个网格图，由 n + 2 条 横线段 和 m + 2 条 竖线段 组成，一开始所有区域均为 1 x 1 的单元格。

所有线段的编号从 1 开始。

给你两个整数 n 和 m 。

同时给你两个整数数组 hBars 和 vBars 。

• hBars 包含区间 [2, n + 1] 内 互不相同 的横线段编号。
• vBars 包含 [2, m + 1] 内 互不相同的 竖线段编号。

如果满足以下条件之一，你可以 移除 两个数组中的部分线段：

• 如果移除的是横线段，它必须是 hBars 中的值。
• 如果移除的是竖线段，它必须是 vBars 中的值。

请你返回移除一些线段后（可能不移除任何线段），剩余网格图中 最大正方形 空洞的面积，正方形空洞的意思是正方形 内部 不含有任何线段。

示例 1：

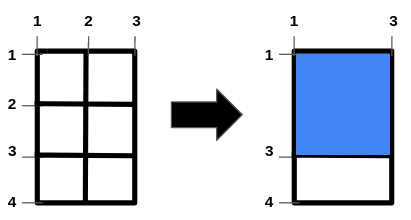
输入：n = 2, m = 1, hBars = [2,3], vBars = [2]
输出：4
解释：左边的图是一开始的网格图。
横线编号的范围是区间 [1,4] ，竖线编号的范围是区间 [1,3] 。
可以移除的横线段为 [2,3] ，竖线段为 [2] 。
一种得到最大正方形面积的方法是移除横线段 2 和竖线段 2 。
操作后得到的网格图如右图所示。
正方形空洞面积为 4。
无法得到面积大于 4 的正方形空洞。
所以答案为 4 。

示例 2：

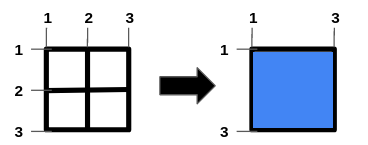
输入：n = 1, m = 1, hBars = [2], vBars = [2]
输出：4
解释：左边的图是一开始的网格图。
横线编号的范围是区间 [1,3] ，竖线编号的范围是区间 [1,3] 。
可以移除的横线段为 [2] ，竖线段为 [2] 。
一种得到最大正方形面积的方法是移除横线段 2 和竖线段 2 。
操作后得到的网格图如右图所示。
正方形空洞面积为 4。
无法得到面积大于 4 的正方形空洞。
所以答案为 4 。

示例 3：

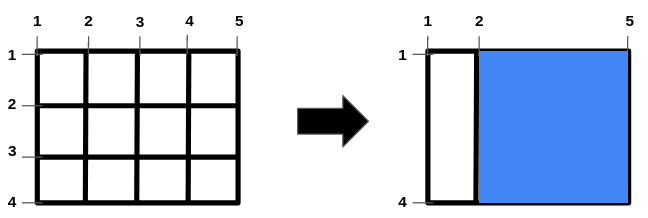
输入：n = 2, m = 3, hBars = [2,3], vBars = [2,3,4]
输出：9
解释：左边的图是一开始的网格图。
横线编号的范围是区间 [1,4] ，竖线编号的范围是区间 [1,5] 。
可以移除的横线段为 [2,3] ，竖线段为 [2,3,4] 。
一种得到最大正方形面积的方法是移除横线段 2、3 和竖线段 3、4 。
操作后得到的网格图如右图所示。
正方形空洞面积为 9。
无法得到面积大于 9 的正方形空洞。
所以答案为 9 。

提示：

• 1 <= n <= 109
• 1 <= m <= 109
• 1 <= hBars.length <= 100
• 2 <= hBars[i] <= n + 1
• 1 <= vBars.length <= 100
• 2 <= vBars[i] <= m + 1
• hBars 中的值互不相同。
• vBars 中的值互不相同。