有一棵由 n 个节点组成的无向树，以 0  为根节点，节点编号从 0 到 n - 1 。给你一个长度为 n - 1 的二维 整数 数组 edges ，其中 edges[i] = [ai, bi] 表示在树上的节点 ai 和 bi 之间存在一条边。另给你一个下标从 0 开始、长度为 n 的数组 coins 和一个整数 k ，其中 coins[i] 表示节点 i 处的金币数量。

从根节点开始，你必须收集所有金币。要想收集节点上的金币，必须先收集该节点的祖先节点上的金币。

节点 i 上的金币可以用下述方法之一进行收集：

• 收集所有金币，得到共计 coins[i] - k 点积分。如果 coins[i] - k 是负数，你将会失去 abs(coins[i] - k) 点积分。
• 收集所有金币，得到共计 floor(coins[i] / 2) 点积分。如果采用这种方法，节点 i 子树中所有节点 j 的金币数 coins[j] 将会减少至 floor(coins[j] / 2) 。

返回收集 所有 树节点的金币之后可以获得的最大积分。

示例 1：

输入：edges = [[0,1],[1,2],[2,3]], coins = [10,10,3,3], k = 5
输出：11                        
解释：
使用第一种方法收集节点 0 上的所有金币。总积分 = 10 - 5 = 5 。
使用第一种方法收集节点 1 上的所有金币。总积分 = 5 + (10 - 5) = 10 。
使用第二种方法收集节点 2 上的所有金币。所以节点 3 上的金币将会变为 floor(3 / 2) = 1 ，总积分 = 10 + floor(3 / 2) = 11 。
使用第二种方法收集节点 3 上的所有金币。总积分 =  11 + floor(1 / 2) = 11.
可以证明收集所有节点上的金币能获得的最大积分是 11 。 

示例 2：

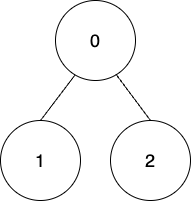
输入：edges = [[0,1],[0,2]], coins = [8,4,4], k = 0
输出：16
解释：
使用第一种方法收集所有节点上的金币，因此，总积分 = (8 - 0) + (4 - 0) + (4 - 0) = 16 。

提示：

• n == coins.length
• 2 <= n <= 105
• 0 <= coins[i] <= 104
• edges.length == n - 1
• 0 <= edges[i][0], edges[i][1] < n
• 0 <= k <= 104