输入: properties = [[1,2],[1,1],[3,4],[4,5],[5,6],[7,7]], k = 1
输出: 3
解释:
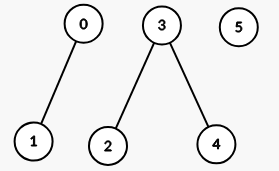
生成的图有 3 个连通分量:
给你一个二维整数数组 properties,其维度为 n x m,以及一个整数 k。
定义一个函数 intersect(a, b),它返回数组 a 和 b 中 共有的不同整数的数量 。
构造一个 无向图,其中每个索引 i 对应 properties[i]。如果且仅当 intersect(properties[i], properties[j]) >= k(其中 i 和 j 的范围为 [0, n - 1] 且 i != j),节点 i 和节点 j 之间有一条边。
返回结果图中 连通分量 的数量。
示例 1:
输入: properties = [[1,2],[1,1],[3,4],[4,5],[5,6],[7,7]], k = 1
输出: 3
解释:
生成的图有 3 个连通分量:

示例 2:
输入: properties = [[1,2,3],[2,3,4],[4,3,5]], k = 2
输出: 1
解释:
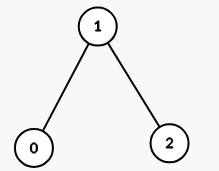
生成的图有 1 个连通分量:
示例 3:
输入: properties = [[1,1],[1,1]], k = 2
输出: 2
解释:
intersect(properties[0], properties[1]) = 1,小于 k。因此在图中 properties[0] 和 properties[1] 之间没有边。
提示:
1 <= n == properties.length <= 1001 <= m == properties[i].length <= 1001 <= properties[i][j] <= 1001 <= k <= m