给你一棵无根带权树，树中总共有 n 个节点，分别表示 n 个服务器，服务器从 0 到 n - 1 编号。同时给你一个数组 edges ，其中 edges[i] = [a_i, b_i, weight_i] 表示节点 a_i 和 b_i 之间有一条双向边，边的权值为 weight_i 。再给你一个整数 signalSpeed 。

如果两台服务器 a 和 b 是通过服务器 c 可连接的，则：

a < b ，a != c 且 b != c 。
从 c 到 a 的距离是可以被 signalSpeed 整除的。
从 c 到 b 的距离是可以被 signalSpeed 整除的。
从 c 到 b 的路径与从 c 到 a 的路径没有任何公共边。

请你返回一个长度为 n 的整数数组 count ，其中 count[i] 表示通过服务器 i 可连接 的服务器对的数目。

示例 1：

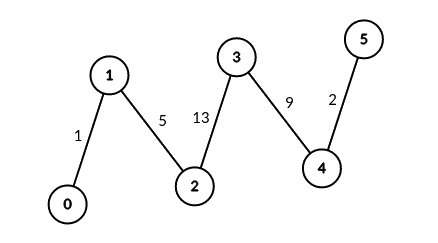
输入：edges = [[0,1,1],[1,2,5],[2,3,13],[3,4,9],[4,5,2]], signalSpeed = 1
输出：[0,4,6,6,4,0]
解释：由于 signalSpeed 等于 1 ，count[c] 等于所有从 c 开始且没有公共边的路径对数目。
在输入图中，count[c] 等于服务器 c 左边服务器数目乘以右边服务器数目。

示例 2：

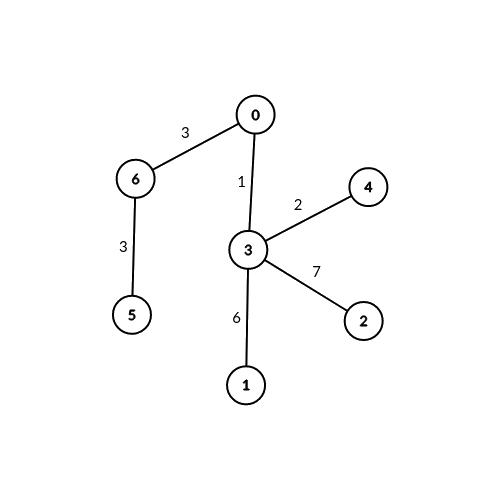
输入：edges = [[0,6,3],[6,5,3],[0,3,1],[3,2,7],[3,1,6],[3,4,2]], signalSpeed = 3
输出：[2,0,0,0,0,0,2]
解释：通过服务器 0 ，有 2 个可连接服务器对(4, 5) 和 (4, 6) 。
通过服务器 6 ，有 2 个可连接服务器对 (4, 5) 和 (0, 5) 。
所有服务器对都必须通过服务器 0 或 6 才可连接，所以其他服务器对应的可连接服务器对数目都为 0 。

提示：

2 <= n <= 1000
edges.length == n - 1
edges[i].length == 3
0 <= a_i, b_i < n
edges[i] = [a_i, b_i, weight_i]
1 <= weight_i <= 10⁶
1 <= signalSpeed <= 10⁶
输入保证 edges 构成一棵合法的树。