给你一个 无向带权 树，共有 n 个节点，编号从 0 到 n - 1。这棵树由一个二维整数数组 edges 表示，长度为 n - 1，其中 edges[i] = [ui, vi, wi] 表示存在一条连接节点 ui 和 vi 的边，权重为 wi。
此外，给你一个二维整数数组 queries，其中 queries[j] = [src1j, src2j, destj]。
返回一个长度等于 queries.length 的数组 answer，其中 answer[j] 表示一个子树的 最小总权重 ，使用该子树的边可以从 src1j 和 src2j 到达 destj 。
这里的 子树 是指原树中任意节点和边组成的连通子集形成的一棵有效树。
示例 1：
输入： edges = [[0,1,2],[1,2,3],[1,3,5],[1,4,4],[2,5,6]], queries = [[2,3,4],[0,2,5]]
输出： [12,11]
解释：
蓝色边表示可以得到最优答案的子树之一。
answer[0]：在选出的子树中，从 src1 = 2 和 src2 = 3 到 dest = 4 的路径总权重为 3 + 5 + 4 = 12。
answer[1]：在选出的子树中，从 src1 = 0 和 src2 = 2 到 dest = 5 的路径总权重为 2 + 3 + 6 = 11。
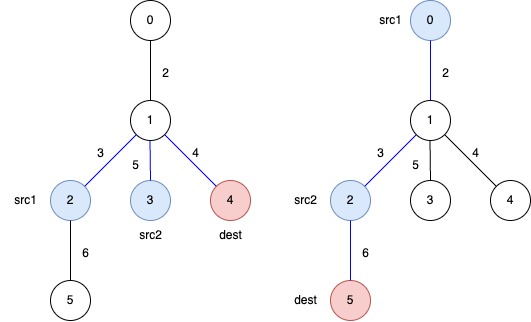
示例 2：
输入： edges = [[1,0,8],[0,2,7]], queries = [[0,1,2]]
输出： [15]
解释：
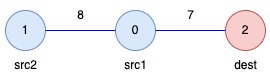
answer[0]：选出的子树中，从 src1 = 0 和 src2 = 1 到 dest = 2 的路径总权重为 8 + 7 = 15。
提示：
3 <= n <= 105edges.length == n - 1edges[i].length == 30 <= ui, vi < n1 <= wi <= 1041 <= queries.length <= 105queries[j].length == 30 <= src1j, src2j, destj < nsrc1j、src2j 和 destj 互不不同。edges 表示的是一棵有效的树。