输入: n = 2, edges = [[0,1,3]], k = 2
输出: 3
解释:
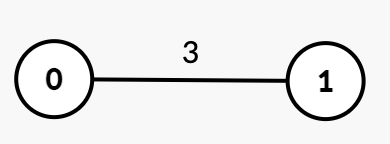
- 最初,图中有一个连通分量
{0, 1}。 - 在
time = 1或2时,图保持不变。 - 在
time = 3时,边[0, 1]被移除,图中形成k = 2个连通分量:{0}和{1}。因此,答案是 3。
给你一个整数 n,表示一个包含 n 个节点(从 0 到 n - 1 编号)的无向图。该图由一个二维数组 edges 表示,其中 edges[i] = [ui, vi, timei] 表示一条连接节点 ui 和节点 vi 的无向边,该边会在时间 timei 被移除。
同时,另给你一个整数 k。
最初,图可能是连通的,也可能是非连通的。你的任务是找到一个 最小 的时间 t,使得在移除所有满足条件 time <= t 的边之后,该图包含 至少 k 个连通分量。
返回这个 最小 时间 t。
连通分量 是图的一个子图,其中任意两个顶点之间都存在路径,且子图中的任意顶点均不与子图外的顶点共享边。
示例 1:
输入: n = 2, edges = [[0,1,3]], k = 2
输出: 3
解释:

{0, 1}。time = 1 或 2 时,图保持不变。time = 3 时,边 [0, 1] 被移除,图中形成 k = 2 个连通分量:{0} 和 {1}。因此,答案是 3。示例 2:
输入: n = 3, edges = [[0,1,2],[1,2,4]], k = 3
输出: 4
解释:
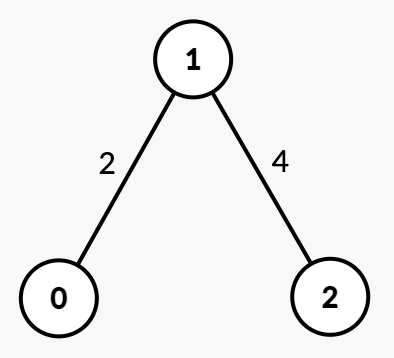
{0, 1, 2}。time = 2 时,边 [0, 1] 被移除,图中形成两个连通分量:{0} 和 {1, 2}。time = 4 时,边 [1, 2] 被移除,图中形成 k = 3 个连通分量:{0}、{1} 和 {2}。因此,答案是 4。示例 3:
输入: n = 3, edges = [[0,2,5]], k = 2
输出: 0
解释:
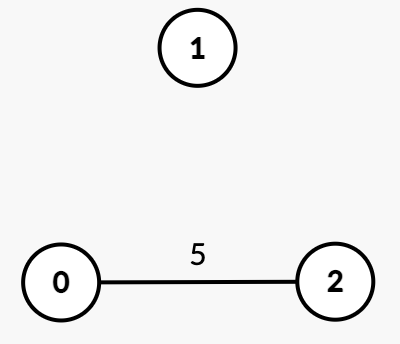
k = 2 个连通分量 {1} 和 {0, 2},无需移除任何边。因此,答案是 0。
提示:
1 <= n <= 1050 <= edges.length <= 105edges[i] = [ui, vi, timei]0 <= ui, vi < nui != vi1 <= timei <= 1091 <= k <= n