输入: squares = [[0,0,1],[2,2,1]]
输出: 1.00000
解释:
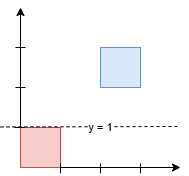
任何在 y = 1 和 y = 2 之间的水平线都会有 1 平方单位的面积在其上方,1 平方单位的面积在其下方。最小的 y 坐标是 1。
给你一个二维整数数组 squares ,其中 squares[i] = [xi, yi, li] 表示一个与 x 轴平行的正方形的左下角坐标和正方形的边长。
找到一个最小的 y 坐标,它对应一条水平线,该线需要满足它以上正方形的总面积 等于 该线以下正方形的总面积。
答案如果与实际答案的误差在 10-5 以内,将视为正确答案。
注意:正方形 可能会 重叠。重叠区域应该被 多次计数 。
示例 1:
输入: squares = [[0,0,1],[2,2,1]]
输出: 1.00000
解释:

任何在 y = 1 和 y = 2 之间的水平线都会有 1 平方单位的面积在其上方,1 平方单位的面积在其下方。最小的 y 坐标是 1。
示例 2:
输入: squares = [[0,0,2],[1,1,1]]
输出: 1.16667
解释:
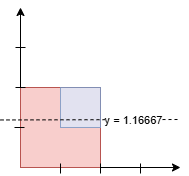
面积如下:
7/6 * 2 (红色) + 1/6 (蓝色) = 15/6 = 2.5。5/6 * 2 (红色) + 5/6 (蓝色) = 15/6 = 2.5。由于线以上和线以下的面积相等,输出为 7/6 = 1.16667。
提示:
1 <= squares.length <= 5 * 104squares[i] = [xi, yi, li]squares[i].length == 30 <= xi, yi <= 1091 <= li <= 1091012。