给你一个正整数 n ，表示总共有 n 个城市，城市从 1 到 n 编号。给你一个二维数组 roads ，其中 roads[i] = [ai, bi, distancei] 表示城市 ai 和 bi 之间有一条 双向 道路，道路距离为 distancei 。城市构成的图不一定是连通的。

两个城市之间一条路径的 分数 定义为这条路径中道路的 最小 距离。

城市 1 和城市 n 之间的所有路径的 最小 分数。

注意：

• 一条路径指的是两个城市之间的道路序列。
• 一条路径可以 多次 包含同一条道路，你也可以沿着路径多次到达城市 1 和城市 n 。
• 测试数据保证城市 1 和城市n 之间 至少 有一条路径。

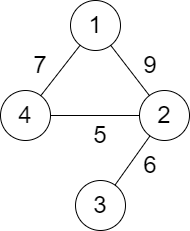
示例 1：

输入：n = 4, roads = [[1,2,9],[2,3,6],[2,4,5],[1,4,7]]
输出：5
解释：城市 1 到城市 4 的路径中，分数最小的一条为：1 -> 2 -> 4 。这条路径的分数是 min(9,5) = 5 。
不存在分数更小的路径。

示例 2：

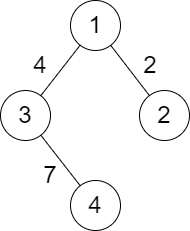
输入：n = 4, roads = [[1,2,2],[1,3,4],[3,4,7]]
输出：2
解释：城市 1 到城市 4 分数最小的路径是：1 -> 2 -> 1 -> 3 -> 4 。这条路径的分数是 min(2,2,4,7) = 2 。

提示：

• 2 <= n <= 105
• 1 <= roads.length <= 105
• roads[i].length == 3
• 1 <= ai, bi <= n
• ai != bi
• 1 <= distancei <= 104
• 不会有重复的边。
• 城市 1 和城市 n 之间至少有一条路径。