You are given an n x n grid where we place some 1 x 1 x 1 cubes that are axis-aligned with the x, y, and z axes.
Each value v = grid[i][j] represents a tower of v cubes placed on top of the cell (i, j).
We view the projection of these cubes onto the xy, yz, and zx planes.
A projection is like a shadow, that maps our 3-dimensional figure to a 2-dimensional plane. We are viewing the "shadow" when looking at the cubes from the top, the front, and the side.
Return the total area of all three projections.
Example 1:
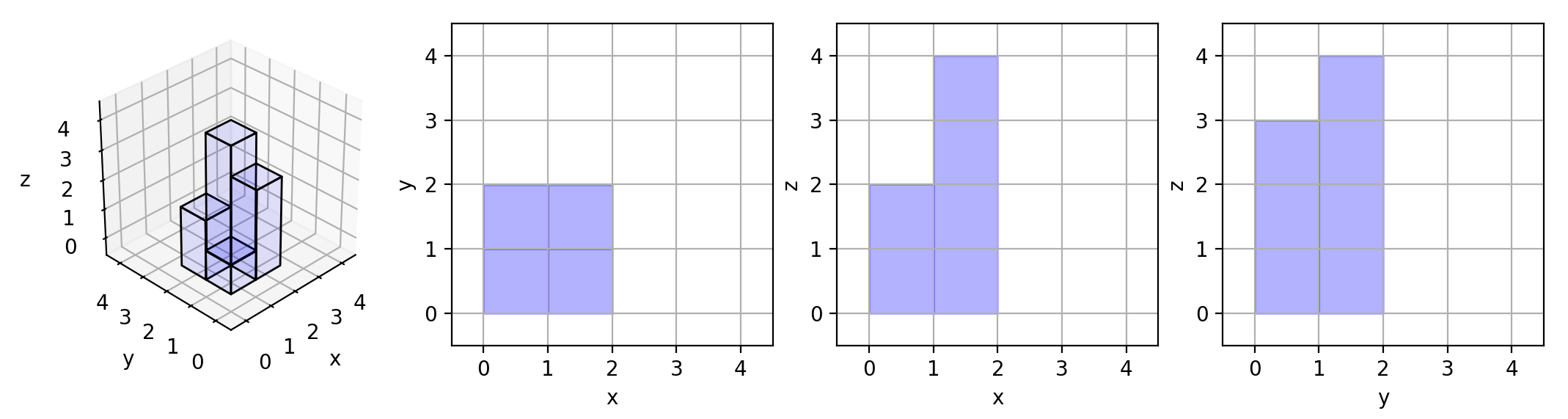
Input: grid = [[1,2],[3,4]]
Output: 17
Explanation: Here are the three projections ("shadows") of the shape made with each axis-aligned plane.
Example 2:
Input: grid = [[2]] Output: 5
Example 3:
Input: grid = [[1,0],[0,2]] Output: 8
Constraints:
n == grid.length == grid[i].length1 <= n <= 500 <= grid[i][j] <= 50