<p>A <strong>peak</strong> element in a 2D grid is an element that is <strong>strictly greater</strong> than all of its <strong>adjacent </strong>neighbors to the left, right, top, and bottom.</p>

<p>Given a <strong>0-indexed</strong> <code>m x n</code> matrix <code>mat</code> where <strong>no two adjacent cells are equal</strong>, find <strong>any</strong> peak element <code>mat[i][j]</code> and return <em>the length 2 array </em><code>[i,j]</code>.</p>

<p>You may assume that the entire matrix is surrounded by an <strong>outer perimeter</strong> with the value <code>-1</code> in each cell.</p>

<p>You must write an algorithm that runs in <code>O(m log(n))</code> or <code>O(n log(m))</code> time.</p>

<p>&nbsp;</p>
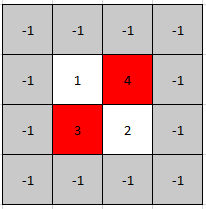
<p><strong>Example 1:</strong></p>

<p><img alt="" src="https://assets.leetcode.com/uploads/2021/06/08/1.png" style="width: 206px; height: 209px;" /></p>

<pre>
<strong>Input:</strong> mat = [[1,4],[3,2]]
<strong>Output:</strong> [0,1]
<strong>Explanation:</strong>&nbsp;Both 3 and 4 are peak elements so [1,0] and [0,1] are both acceptable answers.
</pre>

<p><strong>Example 2:</strong></p>

<p><strong><img alt="" src="https://assets.leetcode.com/uploads/2021/06/07/3.png" style="width: 254px; height: 257px;" /></strong></p>

<pre>
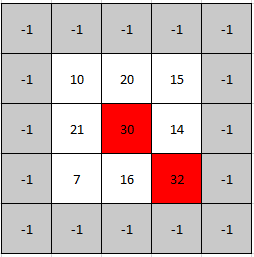
<strong>Input:</strong> mat = [[10,20,15],[21,30,14],[7,16,32]]
<strong>Output:</strong> [1,1]
<strong>Explanation:</strong>&nbsp;Both 30 and 32 are peak elements so [1,1] and [2,2] are both acceptable answers.
</pre>

<p>&nbsp;</p>
<p><strong>Constraints:</strong></p>

<ul>
	<li><code>m == mat.length</code></li>
	<li><code>n == mat[i].length</code></li>
	<li><code>1 &lt;= m, n &lt;= 500</code></li>
	<li><code>1 &lt;= mat[i][j] &lt;= 10<sup>5</sup></code></li>
	<li>No two adjacent cells are equal.</li>
</ul>