There exists an undirected tree with n nodes numbered 0 to n - 1. You are given a 0-indexed 2D integer array edges of length n - 1, where edges[i] = [ui, vi] indicates that there is an edge between nodes ui and vi in the tree. You are also given a positive integer k, and a 0-indexed array of non-negative integers nums of length n, where nums[i] represents the value of the node numbered i.
Alice wants the sum of values of tree nodes to be maximum, for which Alice can perform the following operation any number of times (including zero) on the tree:
[u, v] connecting the nodes u and v, and update their values as follows:
nums[u] = nums[u] XOR knums[v] = nums[v] XOR kReturn the maximum possible sum of the values Alice can achieve by performing the operation any number of times.
Example 1:
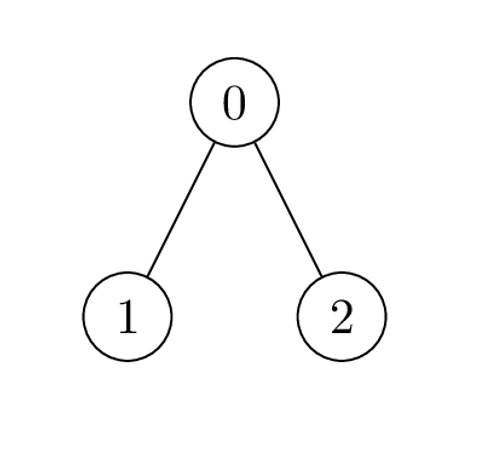
Input: nums = [1,2,1], k = 3, edges = [[0,1],[0,2]] Output: 6 Explanation: Alice can achieve the maximum sum of 6 using a single operation: - Choose the edge [0,2]. nums[0] and nums[2] become: 1 XOR 3 = 2, and the array nums becomes: [1,2,1] -> [2,2,2]. The total sum of values is 2 + 2 + 2 = 6. It can be shown that 6 is the maximum achievable sum of values.
Example 2:
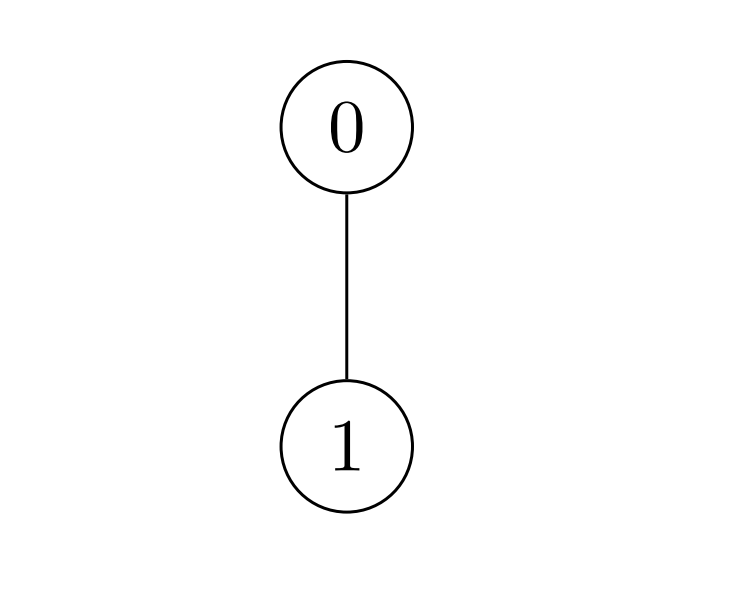
Input: nums = [2,3], k = 7, edges = [[0,1]] Output: 9 Explanation: Alice can achieve the maximum sum of 9 using a single operation: - Choose the edge [0,1]. nums[0] becomes: 2 XOR 7 = 5 and nums[1] become: 3 XOR 7 = 4, and the array nums becomes: [2,3] -> [5,4]. The total sum of values is 5 + 4 = 9. It can be shown that 9 is the maximum achievable sum of values.
Example 3:
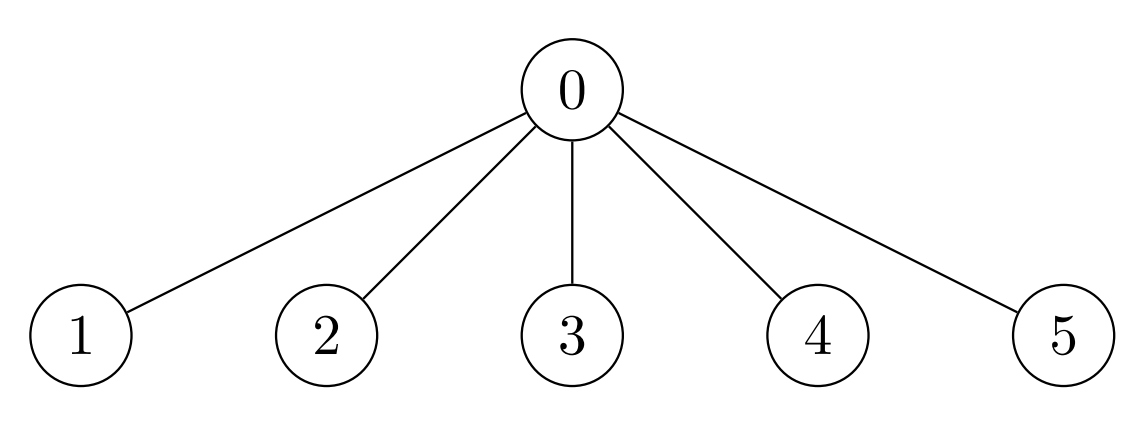
Input: nums = [7,7,7,7,7,7], k = 3, edges = [[0,1],[0,2],[0,3],[0,4],[0,5]] Output: 42 Explanation: The maximum achievable sum is 42 which can be achieved by Alice performing no operations.
Constraints:
2 <= n == nums.length <= 2 * 1041 <= k <= 1090 <= nums[i] <= 109edges.length == n - 1edges[i].length == 20 <= edges[i][0], edges[i][1] <= n - 1edges represent a valid tree.