There exist n rectangles in a 2D plane. You are given two 0-indexed 2D integer arrays bottomLeft and topRight, both of size n x 2, where bottomLeft[i] and topRight[i] represent the bottom-left and top-right coordinates of the ith rectangle respectively.
You can select a region formed from the intersection of two of the given rectangles. You need to find the largest area of a square that can fit inside this region if you select the region optimally.
Return the largest possible area of a square, or 0 if there do not exist any intersecting regions between the rectangles.
Example 1:
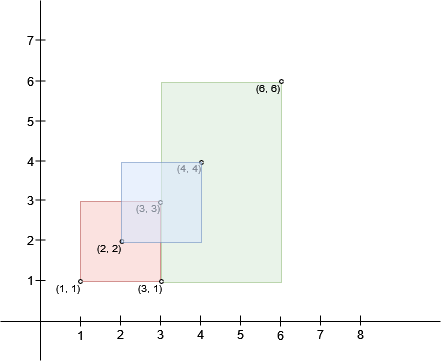
Input: bottomLeft = [[1,1],[2,2],[3,1]], topRight = [[3,3],[4,4],[6,6]] Output: 1 Explanation: A square with side length 1 can fit inside either the intersecting region of rectangle 0 and rectangle 1, or the intersecting region of rectangle 1 and rectangle 2. Hence the largest area is side * side which is 1 * 1 == 1. It can be shown that a square with a greater side length can not fit inside any intersecting region.
Example 2:
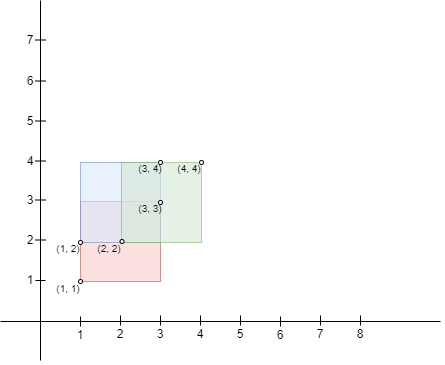
Input: bottomLeft = [[1,1],[2,2],[1,2]], topRight = [[3,3],[4,4],[3,4]] Output: 1 Explanation: A square with side length 1 can fit inside either the intersecting region of rectangle 0 and rectangle 1, the intersecting region of rectangle 1 and rectangle 2, or the intersection region of all 3 rectangles. Hence the largest area is side * side which is 1 * 1 == 1. It can be shown that a square with a greater side length can not fit inside any intersecting region. Note that the region can be formed by the intersection of more than 2 rectangles.
Example 3:
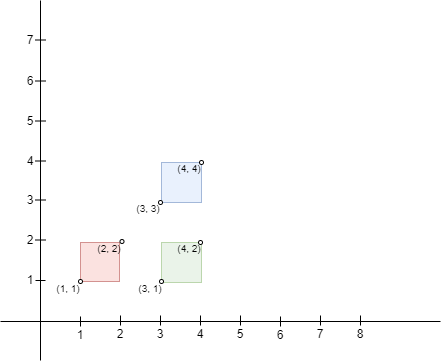
Input: bottomLeft = [[1,1],[3,3],[3,1]], topRight = [[2,2],[4,4],[4,2]] Output: 0 Explanation: No pair of rectangles intersect, hence, we return 0.
Constraints:
n == bottomLeft.length == topRight.length2 <= n <= 103bottomLeft[i].length == topRight[i].length == 21 <= bottomLeft[i][0], bottomLeft[i][1] <= 1071 <= topRight[i][0], topRight[i][1] <= 107bottomLeft[i][0] < topRight[i][0]bottomLeft[i][1] < topRight[i][1]