You are given a non-negative integer n representing a 2ⁿ x 2ⁿ grid. You must fill the grid with integers from 0 to 2²ⁿ - 1 to make it special. A grid is special if it satisfies all the following conditions:

All numbers in the top-right quadrant are smaller than those in the bottom-right quadrant.
All numbers in the bottom-right quadrant are smaller than those in the bottom-left quadrant.
All numbers in the bottom-left quadrant are smaller than those in the top-left quadrant.
Each of its quadrants is also a special grid.

Return the special 2ⁿ x 2ⁿ grid.

Note: Any 1x1 grid is special.

Example 1:

Input: n = 0

Output: [[0]]

Explanation:

The only number that can be placed is 0, and there is only one possible position in the grid.

Example 2:

Input: n = 1

Output: [[3,0],[2,1]]

Explanation:

The numbers in each quadrant are:

Top-right: 0
Bottom-right: 1
Bottom-left: 2
Top-left: 3

Since 0 < 1 < 2 < 3, this satisfies the given constraints.

Example 3:

Input: n = 2

Output: [[15,12,3,0],[14,13,2,1],[11,8,7,4],[10,9,6,5]]

Explanation:

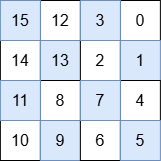
The numbers in each quadrant are:

Top-right: 3, 0, 2, 1
Bottom-right: 7, 4, 6, 5
Bottom-left: 11, 8, 10, 9
Top-left: 15, 12, 14, 13
max(3, 0, 2, 1) < min(7, 4, 6, 5)
max(7, 4, 6, 5) < min(11, 8, 10, 9)
max(11, 8, 10, 9) < min(15, 12, 14, 13)

This satisfies the first three requirements. Additionally, each quadrant is also a special grid. Thus, this is a special grid.

Constraints:

0 <= n <= 10