输入: coords = [[1,1],[1,2],[3,2],[3,3]]
输出: 2
解释:
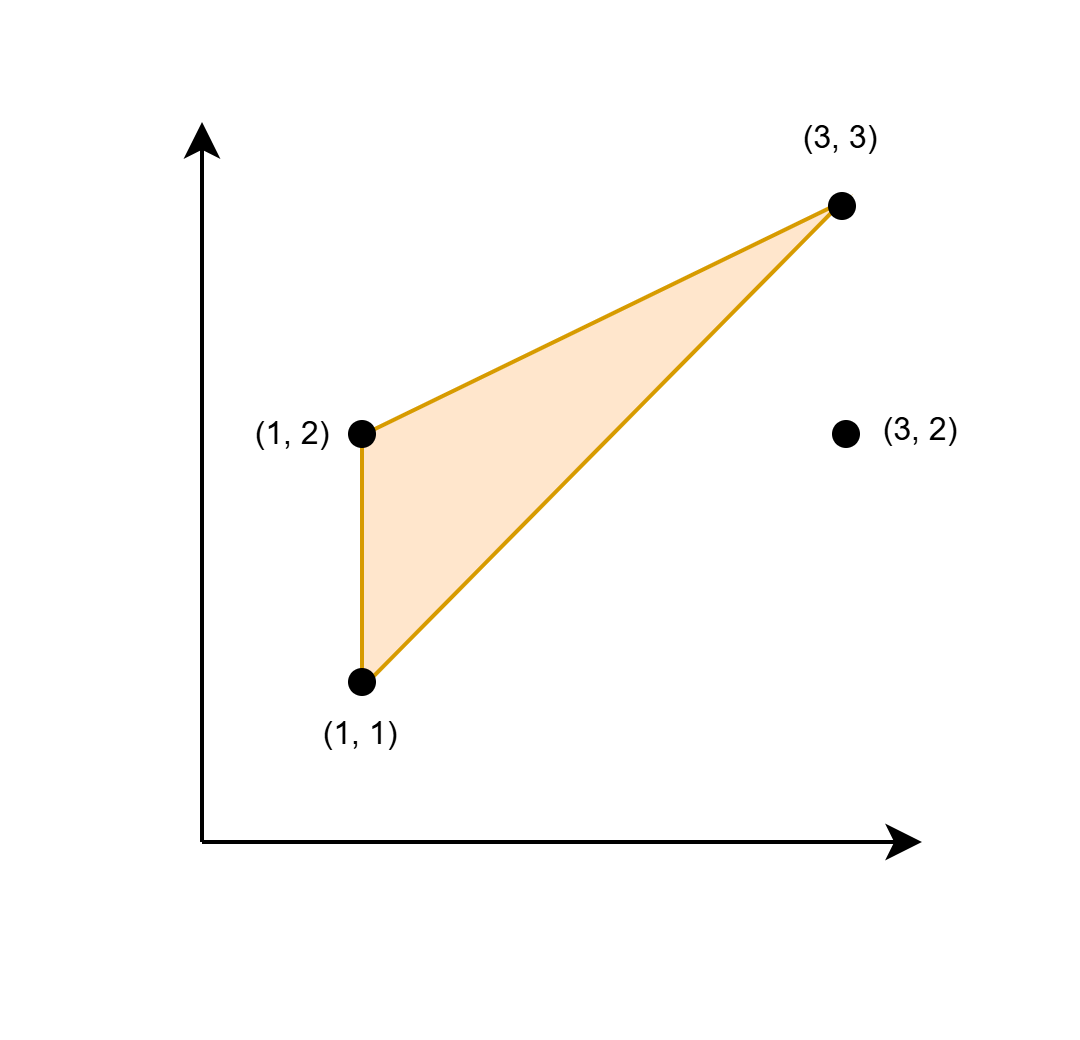
图中的三角形的底边为 1,高为 2。因此,它的面积为 1/2 * 底边 * 高 = 1。
给你一个二维数组 coords,大小为 n x 2,表示一个无限笛卡尔平面上 n 个点的坐标。
找出一个 最大 三角形的 两倍 面积,其中三角形的三个顶点来自 coords 中的任意三个点,并且该三角形至少有一条边与 x 轴或 y 轴平行。严格地说,如果该三角形的最大面积为 A,则返回 2 * A。
如果不存在这样的三角形,返回 -1。
注意,三角形的面积 不能 为零。
示例 1:
输入: coords = [[1,1],[1,2],[3,2],[3,3]]
输出: 2
解释:

图中的三角形的底边为 1,高为 2。因此,它的面积为 1/2 * 底边 * 高 = 1。
示例 2:
输入: coords = [[1,1],[2,2],[3,3]]
输出: -1
解释:
唯一可能的三角形的顶点是 (1, 1)、(2, 2) 和 (3, 3)。它的任意边都不与 x 轴或 y 轴平行。
提示:
1 <= n == coords.length <= 1051 <= coords[i][0], coords[i][1] <= 106coords[i] 都是 唯一 的。