给你一个有 n 个节点的 有向带权 图,节点编号为 0 到 n - 1 。图中的初始边用数组 edges 表示,其中 edges[i] = [fromi, toi, edgeCosti] 表示从 fromi 到 toi 有一条代价为 edgeCosti 的边。
请你实现一个 Graph 类:
Graph(int n, int[][] edges) 初始化图有 n 个节点,并输入初始边。addEdge(int[] edge) 向边集中添加一条边,其中 edge = [from, to, edgeCost] 。数据保证添加这条边之前对应的两个节点之间没有有向边。int shortestPath(int node1, int node2) 返回从节点 node1 到 node2 的路径 最小 代价。如果路径不存在,返回 -1 。一条路径的代价是路径中所有边代价之和。
示例 1:

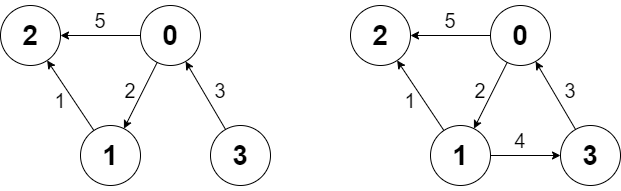
输入: ["Graph", "shortestPath", "shortestPath", "addEdge", "shortestPath"] [[4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]], [3, 2], [0, 3], [[1, 3, 4]], [0, 3]] 输出: [null, 6, -1, null, 6] 解释: Graph g = new Graph(4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]); g.shortestPath(3, 2); // 返回 6 。从 3 到 2 的最短路径如第一幅图所示:3 -> 0 -> 1 -> 2 ,总代价为 3 + 2 + 1 = 6 。 g.shortestPath(0, 3); // 返回 -1 。没有从 0 到 3 的路径。 g.addEdge([1, 3, 4]); // 添加一条节点 1 到节点 3 的边,得到第二幅图。 g.shortestPath(0, 3); // 返回 6 。从 0 到 3 的最短路径为 0 -> 1 -> 3 ,总代价为 2 + 4 = 6 。
提示:
1 <= n <= 1000 <= edges.length <= n * (n - 1)edges[i].length == edge.length == 30 <= fromi, toi, from, to, node1, node2 <= n - 11 <= edgeCosti, edgeCost <= 106addEdge 至多 100 次。shortestPath 至多 100 次。