输入:parent = [-1,0,0,1,1,1], s = "abaabc"
输出:[6,3,1,1,1,1]
解释:
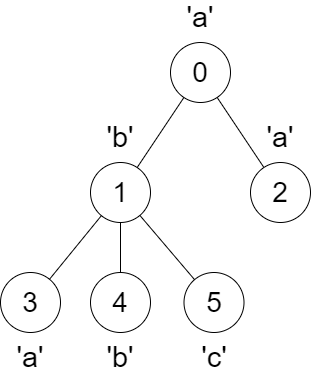
节点 3 的父节点从节点 1 变为节点 0 。
给你一棵 n 个节点且根节点为编号 0 的树,节点编号为 0 到 n - 1 。这棵树用一个长度为 n 的数组 parent 表示,其中 parent[i] 是第 i 个节点的父亲节点的编号。由于节点 0 是根,parent[0] == -1 。
给你一个长度为 n 的字符串 s ,其中 s[i] 是节点 i 对应的字符。
对于节点编号从 1 到 n - 1 的每个节点 x ,我们 同时 执行以下操作 一次 :
x 最近 的祖先节点 y ,且 s[x] == s[y] 。y 不存在,那么不做任何修改。x 与它父亲节点之间的边 删除 ,在 x 与 y 之间连接一条边,使 y 变为 x 新的父节点。请你返回一个长度为 n 的数组 answer ,其中 answer[i] 是 最终 树中,节点 i 为根的 子树 的 大小 。
示例 1:
输入:parent = [-1,0,0,1,1,1], s = "abaabc"
输出:[6,3,1,1,1,1]
解释:

节点 3 的父节点从节点 1 变为节点 0 。
示例 2:
输入:parent = [-1,0,4,0,1], s = "abbba"
输出:[5,2,1,1,1]
解释:
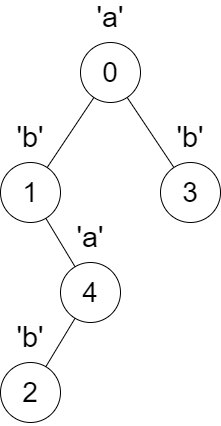
以下变化会同时发生:
提示:
n == parent.length == s.length1 <= n <= 105i >= 1 ,都有 0 <= parent[i] <= n - 1 。parent[0] == -1parent 表示一棵合法的树。s 只包含小写英文字母。