You are given a m x n matrix grid. Initially, you are located at the top-left corner (0, 0), and in each step, you can only move right or down in the matrix.
Among all possible paths starting from the top-left corner (0, 0) and ending in the bottom-right corner (m - 1, n - 1), find the path with the maximum non-negative product. The product of a path is the product of all integers in the grid cells visited along the path.
Return the maximum non-negative product modulo 109 + 7. If the maximum product is negative, return -1.
Notice that the modulo is performed after getting the maximum product.
Example 1:
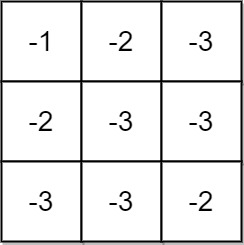
Input: grid = [[-1,-2,-3],[-2,-3,-3],[-3,-3,-2]] Output: -1 Explanation: It is not possible to get non-negative product in the path from (0, 0) to (2, 2), so return -1.
Example 2:
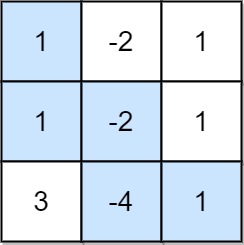
Input: grid = [[1,-2,1],[1,-2,1],[3,-4,1]] Output: 8 Explanation: Maximum non-negative product is shown (1 * 1 * -2 * -4 * 1 = 8).
Example 3:
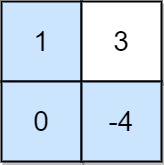
Input: grid = [[1,3],[0,-4]] Output: 0 Explanation: Maximum non-negative product is shown (1 * 0 * -4 = 0).
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 15-4 <= grid[i][j] <= 4