给你一个二维整数数组 rectangles ，其中 rectangles[i] = [li, hi] 表示第 i 个矩形长为 li 高为 hi 。给你一个二维整数数组 points ，其中 points[j] = [xj, yj] 是坐标为 (xj, yj) 的一个点。

第 i 个矩形的 左下角 在 (0, 0) 处，右上角 在 (li, hi) 。

请你返回一个整数数组 count ，长度为 points.length，其中 count[j]是 包含 第 j 个点的矩形数目。

如果 0 <= xj <= li 且 0 <= yj <= hi ，那么我们说第 i 个矩形包含第 j 个点。如果一个点刚好在矩形的 边上 ，这个点也被视为被矩形包含。

 

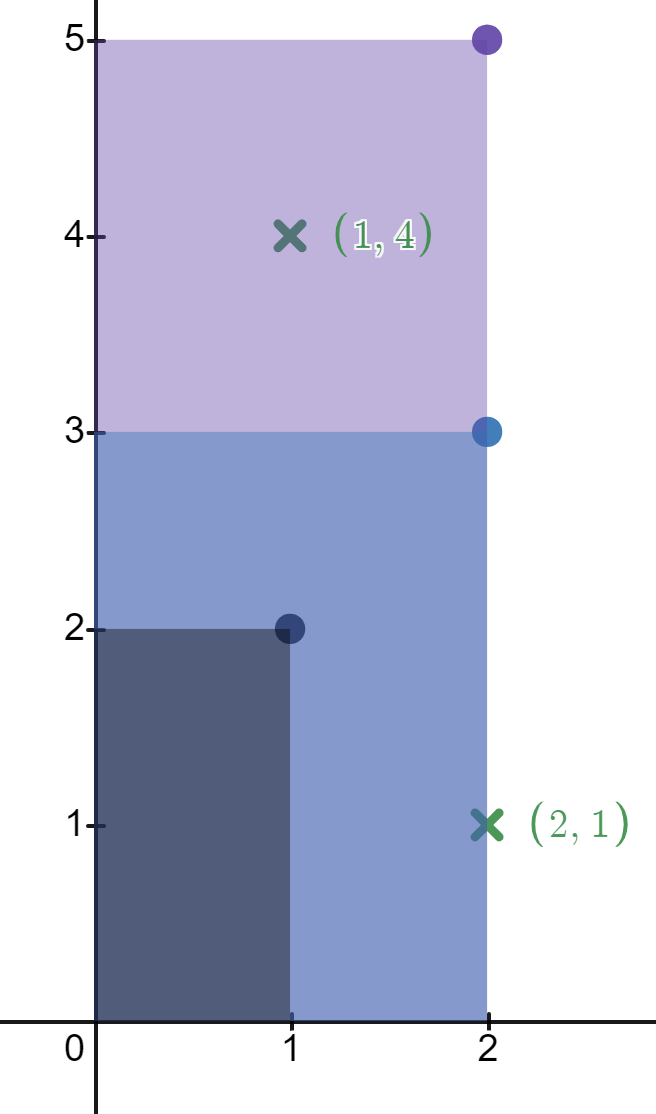
示例 1：

输入：rectangles = [[1,2],[2,3],[2,5]], points = [[2,1],[1,4]]
输出：[2,1]
解释：
第一个矩形不包含任何点。
第二个矩形只包含一个点 (2, 1) 。
第三个矩形包含点 (2, 1) 和 (1, 4) 。
包含点 (2, 1) 的矩形数目为 2 。
包含点 (1, 4) 的矩形数目为 1 。
所以，我们返回 [2, 1] 。

示例 2：

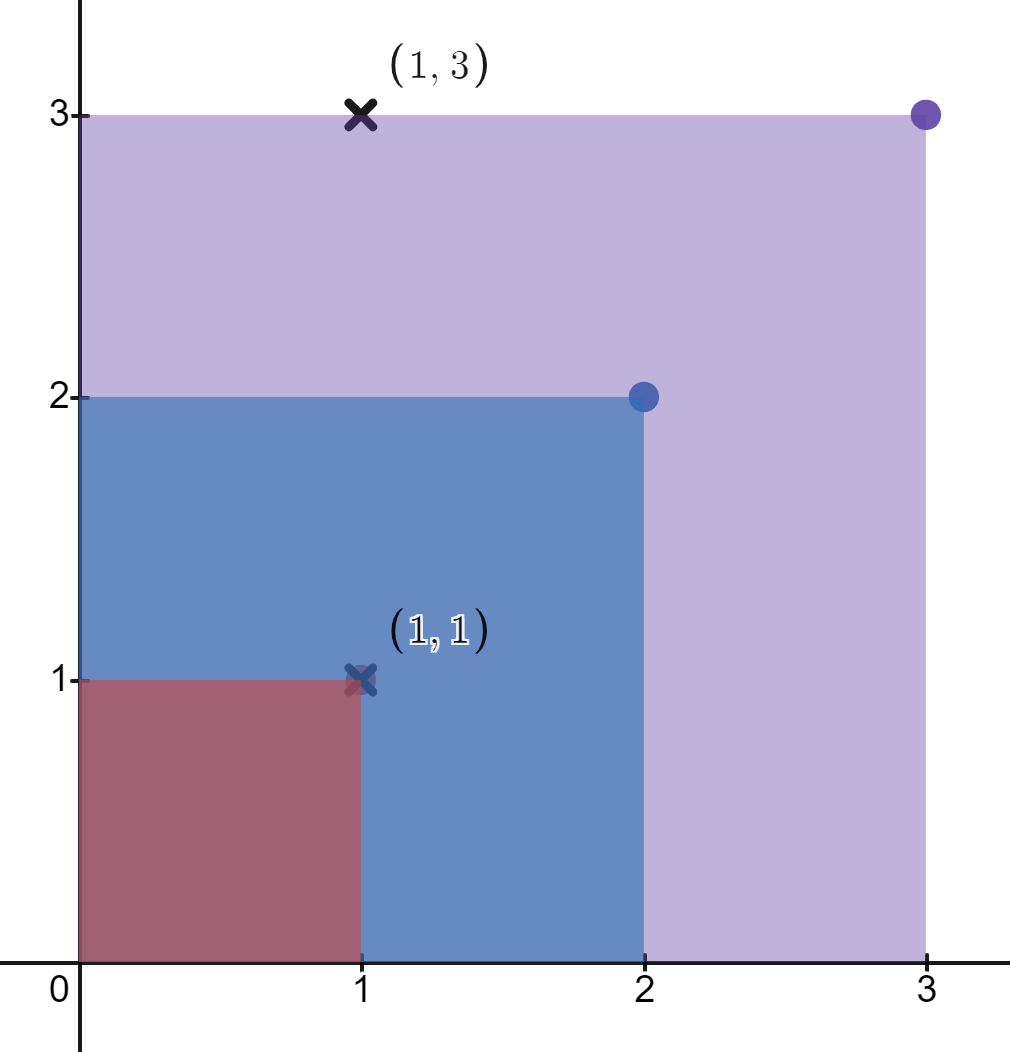
输入：rectangles = [[1,1],[2,2],[3,3]], points = [[1,3],[1,1]]
输出：[1,3]
解释：
第一个矩形只包含点 (1, 1) 。
第二个矩形只包含点 (1, 1) 。
第三个矩形包含点 (1, 3) 和 (1, 1) 。
包含点 (1, 3) 的矩形数目为 1 。
包含点 (1, 1) 的矩形数目为 3 。
所以，我们返回 [1, 3] 。

 

提示：