给你一个正整数 n ，表示一个无向图中的节点数目，节点编号从 1 到 n 。

同时给你一个二维整数数组 edges ，其中 edges[i] = [a_i,b_i] 表示节点 a_i 和 b_i之间有一条双向边。注意给定的图可能是不连通的。

请你将图划分为 m 个组（编号从 1 开始），满足以下要求：

图中每个节点都只属于一个组。
图中每条边连接的两个点 [a_i,b_i] ，如果 a_i 属于编号为 x 的组，b_i 属于编号为 y 的组，那么 |y - x| = 1 。

请你返回最多可以将节点分为多少个组（也就是最大的 m ）。如果没办法在给定条件下分组，请你返回 -1 。

示例 1：

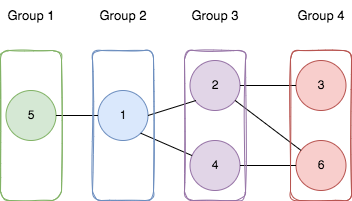
输入：n = 6, edges = [[1,2],[1,4],[1,5],[2,6],[2,3],[4,6]]
输出：4
解释：如上图所示，
- 节点 5 在第一个组。
- 节点 1 在第二个组。
- 节点 2 和节点 4 在第三个组。
- 节点 3 和节点 6 在第四个组。
所有边都满足题目要求。
如果我们创建第五个组，将第三个组或者第四个组中任何一个节点放到第五个组，至少有一条边连接的两个节点所属的组编号不符合题目要求。

示例 2：

输入：n = 3, edges = [[1,2],[2,3],[3,1]]
输出：-1
解释：如果我们将节点 1 放入第一个组，节点 2 放入第二个组，节点 3 放入第三个组，前两条边满足题目要求，但第三条边不满足题目要求。
没有任何符合题目要求的分组方式。

提示：

1 <= n <= 500
1 <= edges.length <= 10⁴
edges[i].length == 2
1 <= a_i, b_i <= n
a_i != b_i
两个点之间至多只有一条边。