You are given an array points where points[i] = [xi, yi] is the coordinates of the ith point on a 2D plane. Multiple points can have the same coordinates.

You are also given an array queries where queries[j] = [xj, yj, rj] describes a circle centered at (xj, yj) with a radius of rj.

For each query queries[j], compute the number of points inside the jth circle. Points on the border of the circle are considered inside.

Return an array answer, where answer[j] is the answer to the jth query.

Example 1:

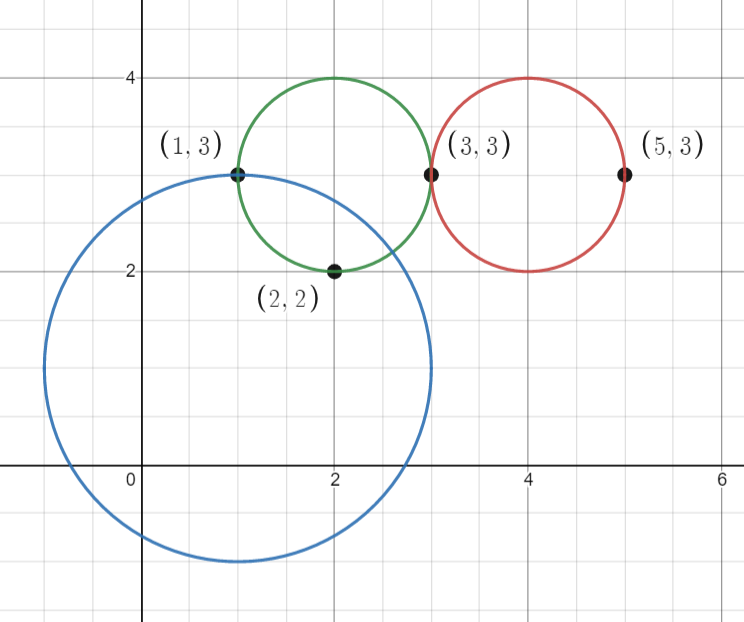
Input: points = [[1,3],[3,3],[5,3],[2,2]], queries = [[2,3,1],[4,3,1],[1,1,2]]
Output: [3,2,2]
Explanation: The points and circles are shown above.
queries[0] is the green circle, queries[1] is the red circle, and queries[2] is the blue circle.

Example 2:

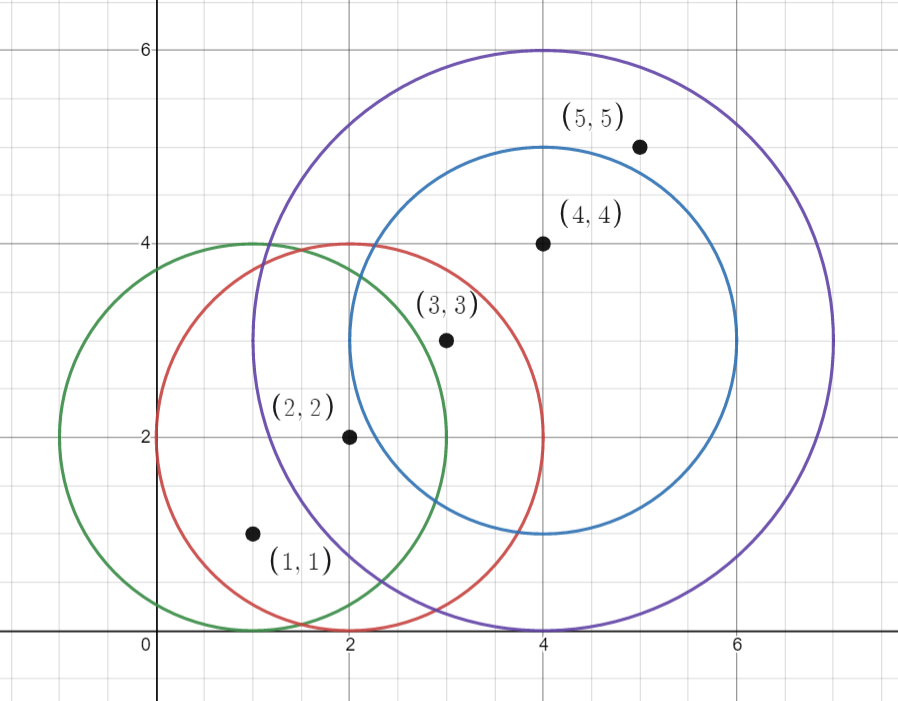
Input: points = [[1,1],[2,2],[3,3],[4,4],[5,5]], queries = [[1,2,2],[2,2,2],[4,3,2],[4,3,3]]
Output: [2,3,2,4]
Explanation: The points and circles are shown above.
queries[0] is green, queries[1] is red, queries[2] is blue, and queries[3] is purple.

Constraints:

• 1 <= points.length <= 500
• points[i].length == 2
• 0 <= x​​​​​​i, y​​​​​​i <= 500
• 1 <= queries.length <= 500
• queries[j].length == 3
• 0 <= xj, yj <= 500
• 1 <= rj <= 500
• All coordinates are integers.

Follow up: Could you find the answer for each query in better complexity than O(n)?