输入:edges = [[0,1],[0,2]]
输出:[2,4,3]
解释:
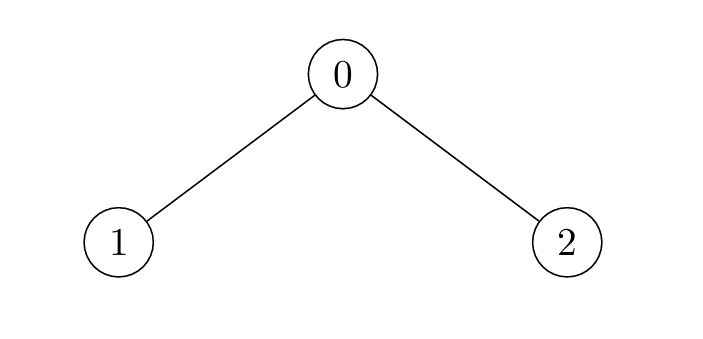
- 对于
i = 0:- 节点 1 在时刻
t = 1被标记,节点 2 在时刻t = 2被标记。
- 节点 1 在时刻
- 对于
i = 1:- 节点 0 在时刻
t = 2被标记,节点 2 在时刻t = 4被标记。
- 节点 0 在时刻
- 对于
i = 2:- 节点 0 在时刻
t = 2被标记,节点 1 在时刻t = 3被标记。
- 节点 0 在时刻
给你一棵 无向 树,树中节点从 0 到 n - 1 编号。同时给你一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ui, vi] 表示节点 ui 和 vi 在树中有一条边。
一开始,所有 节点都 未标记 。对于节点 i :
i 是奇数时,如果时刻 x - 1 该节点有 至少 一个相邻节点已经被标记了,那么节点 i 会在时刻 x 被标记。i 是偶数时,如果时刻 x - 2 该节点有 至少 一个相邻节点已经被标记了,那么节点 i 会在时刻 x 被标记。请你返回一个数组 times ,表示如果你在时刻 t = 0 标记节点 i ,那么时刻 times[i] 时,树中所有节点都会被标记。
请注意,每个 times[i] 的答案都是独立的,即当你标记节点 i 时,所有其他节点都未标记。
示例 1:
输入:edges = [[0,1],[0,2]]
输出:[2,4,3]
解释:

i = 0 :
t = 1 被标记,节点 2 在时刻 t = 2 被标记。i = 1 :
t = 2 被标记,节点 2 在时刻 t = 4 被标记。i = 2 :
t = 2 被标记,节点 1 在时刻 t = 3 被标记。示例 2:
输入:edges = [[0,1]]
输出:[1,2]
解释:
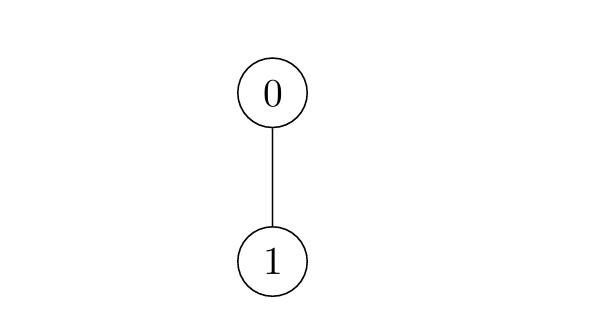
i = 0 :
t = 1 被标记。i = 1 :
t = 2 被标记。示例 3:
输入:edges = [[2,4],[0,1],[2,3],[0,2]]
输出:[4,6,3,5,5]
解释:
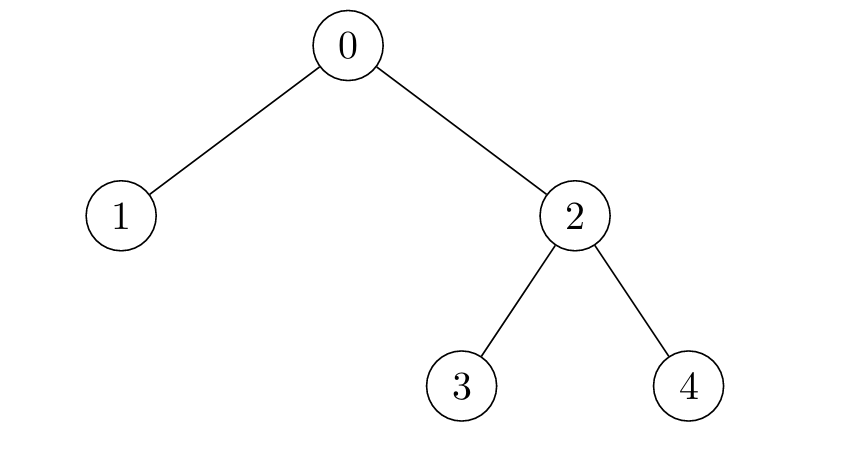
提示:
2 <= n <= 105edges.length == n - 1edges[i].length == 20 <= edges[i][0], edges[i][1] <= n - 1edges 表示一棵合法的树。