存在一个 n x n 大小、下标从 0 开始的网格，网格中埋着一些工件。给你一个整数 n 和一个下标从 0 开始的二维整数数组 artifacts ，artifacts 描述了矩形工件的位置，其中 artifacts[i] = [r1i, c1i, r2i, c2i] 表示第 i 个工件在子网格中的填埋情况：

你将会挖掘网格中的一些单元格，并清除其中的填埋物。如果单元格中埋着工件的一部分，那么该工件这一部分将会裸露出来。如果一个工件的所有部分都都裸露出来，你就可以提取该工件。

给你一个下标从 0 开始的二维整数数组 dig ，其中 dig[i] = [ri, ci] 表示你将会挖掘单元格 (ri, ci) ，返回你可以提取的工件数目。

生成的测试用例满足：

 

示例 1：

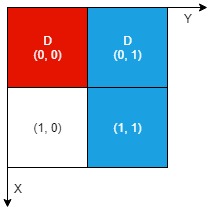
输入：n = 2, artifacts = [[0,0,0,0],[0,1,1,1]], dig = [[0,0],[0,1]]
输出：1
解释： 
不同颜色表示不同的工件。挖掘的单元格用 'D' 在网格中进行标记。
有 1 个工件可以提取，即红色工件。
蓝色工件在单元格 (1,1) 的部分尚未裸露出来，所以无法提取该工件。
因此，返回 1 。

示例 2：

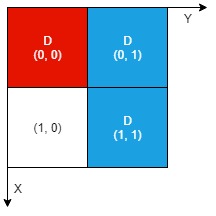
输入：n = 2, artifacts = [[0,0,0,0],[0,1,1,1]], dig = [[0,0],[0,1],[1,1]]
输出：2
解释：红色工件和蓝色工件的所有部分都裸露出来（用 'D' 标记），都可以提取。因此，返回 2 。

 

提示：