给你一个 n 个节点的 有向图 ，节点编号为 0 到 n - 1 ，每个节点至多有一条出边。

有向图用大小为 n 下标从 0 开始的数组 edges 表示，表示节点 i 有一条有向边指向 edges[i] 。如果节点 i 没有出边，那么 edges[i] == -1 。

同时给你两个节点 node1 和 node2 。

请你返回一个从 node1 和 node2 都能到达节点的编号，使节点 node1 和节点 node2 到这个节点的距离 较大值最小化。如果有多个答案，请返回最小的节点编号。如果答案不存在，返回 -1 。

注意 edges 可能包含环。

示例 1：

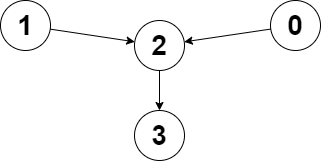
输入：edges = [2,2,3,-1], node1 = 0, node2 = 1
输出：2
解释：从节点 0 到节点 2 的距离为 1 ，从节点 1 到节点 2 的距离为 1 。
两个距离的较大值为 1 。我们无法得到一个比 1 更小的较大值，所以我们返回节点 2 。

示例 2：

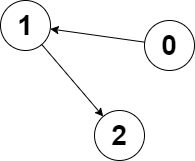
输入：edges = [1,2,-1], node1 = 0, node2 = 2
输出：2
解释：节点 0 到节点 2 的距离为 2 ，节点 2 到它自己的距离为 0 。
两个距离的较大值为 2 。我们无法得到一个比 2 更小的较大值，所以我们返回节点 2 。

提示：