<p>Alice 和 Bob 是一场射箭比赛中的对手。比赛规则如下：</p>

<ol>
	<li>Alice 先射 <code>numArrows</code> 支箭，然后 Bob 也射 <code>numArrows</code> 支箭。</li>
	<li>分数按下述规则计算：
	<ol>
		<li>箭靶有若干整数计分区域，范围从 <code>0</code> 到 <code>11</code> （含 <code>0</code> 和 <code>11</code>）。</li>
		<li>箭靶上每个区域都对应一个得分 <code>k</code>（范围是 <code>0</code> 到 <code>11</code>），Alice 和 Bob 分别在得分 <code>k</code>&nbsp;区域射中&nbsp;<code>a<sub>k</sub></code> 和 <code>b<sub>k</sub></code> 支箭。如果 <code>a<sub>k</sub> &gt;= b<sub>k</sub></code> ，那么 Alice 得 <code>k</code> 分。如果 <code>a<sub>k</sub> &lt; b<sub>k</sub></code> ，则 Bob 得 <code>k</code> 分</li>
		<li>如果 <code>a<sub>k</sub> == b<sub>k</sub> == 0</code> ，那么无人得到 <code>k</code> 分。</li>
	</ol>
	</li>
</ol>

<ul>
	<li>
	<p>例如，Alice 和 Bob 都向计分为 <code>11</code> 的区域射 <code>2</code> 支箭，那么 Alice 得 <code>11</code> 分。如果 Alice 向计分为 <code>11</code> 的区域射 <code>0</code> 支箭，但 Bob 向同一个区域射 <code>2</code> 支箭，那么 Bob 得&nbsp;<code>11</code> 分。</p>
	</li>
</ul>

<p>给你整数 <code>numArrows</code> 和一个长度为 <code>12</code> 的整数数组 <code>aliceArrows</code> ，该数组表示 Alice 射中&nbsp;<code>0</code> 到 <code>11</code> 每个计分区域的箭数量。现在，Bob 想要尽可能 <strong>最大化</strong> 他所能获得的总分。</p>

<p>返回数组 <code>bobArrows</code><em> </em>，该数组表示 Bob 射中&nbsp;<code>0</code> 到 <code>11</code> <strong>每个</strong> 计分区域的箭数量。且 <code>bobArrows</code> 的总和应当等于 <code>numArrows</code> 。</p>

<p>如果存在多种方法都可以使 Bob 获得最大总分，返回其中 <strong>任意一种</strong> 即可。</p>

<p>&nbsp;</p>

<p><strong>示例 1：</strong></p>

<p><img alt="" src="https://pic.leetcode-cn.com/1647744752-kQKrXw-image.png" style="width: 600px; height: 120px;" /></p>

<pre>
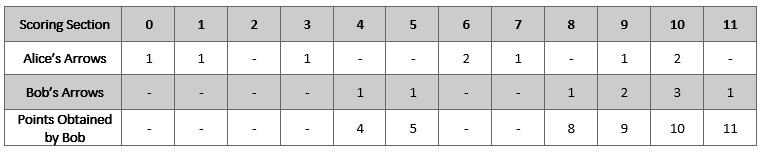
<strong>输入：</strong>numArrows = 9, aliceArrows = [1,1,0,1,0,0,2,1,0,1,2,0]
<strong>输出：</strong>[0,0,0,0,1,1,0,0,1,2,3,1]
<strong>解释：</strong>上表显示了比赛得分情况。
Bob 获得总分 4 + 5 + 8 + 9 + 10 + 11 = 47 。
可以证明 Bob 无法获得比 47 更高的分数。
</pre>

<p><strong>示例 2：</strong></p>

<p><img alt="" src="https://pic.leetcode-cn.com/1647744785-cMHzaC-image.png" style="width: 600px; height: 117px;" /></p>

<pre>
<strong>输入：</strong>numArrows = 3, aliceArrows = [0,0,1,0,0,0,0,0,0,0,0,2]
<strong>输出：</strong>[0,0,0,0,0,0,0,0,1,1,1,0]
<strong>解释：</strong>上表显示了比赛得分情况。
Bob 获得总分 8 + 9 + 10 = 27 。
可以证明 Bob 无法获得比 27 更高的分数。
</pre>

<p>&nbsp;</p>

<p><strong>提示：</strong></p>

<ul>
	<li><code>1 &lt;= numArrows &lt;= 10<sup>5</sup></code></li>
	<li><code>aliceArrows.length == bobArrows.length == 12</code></li>
	<li><code>0 &lt;= aliceArrows[i], bobArrows[i] &lt;= numArrows</code></li>
	<li><code>sum(aliceArrows[i]) == numArrows</code></li>
</ul>