给你一个下标从 0 开始、大小为 n x n 的矩阵 grid ，其中 n 为奇数，且 grid[r][c] 的值为 0 、1 或 2 。

如果一个单元格属于以下三条线中的任一一条，我们就认为它是字母 Y 的一部分：

• 从左上角单元格开始到矩阵中心单元格结束的对角线。
• 从右上角单元格开始到矩阵中心单元格结束的对角线。
• 从中心单元格开始到矩阵底部边界结束的垂直线。

当且仅当满足以下全部条件时，可以判定矩阵上写有字母 Y ：

• 属于 Y 的所有单元格的值相等。
• 不属于 Y 的所有单元格的值相等。
• 属于 Y 的单元格的值与不属于Y的单元格的值不同。

每次操作你可以将任意单元格的值改变为 0 、1 或 2 。返回在矩阵上写出字母 Y 所需的 最少 操作次数。

示例 1：

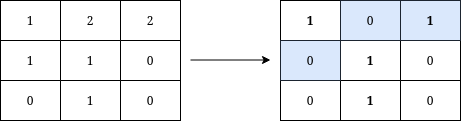
输入：grid = [[1,2,2],[1,1,0],[0,1,0]]
输出：3
解释：将在矩阵上写出字母 Y 需要执行的操作用蓝色高亮显示。操作后，所有属于 Y 的单元格（加粗显示）的值都为 1 ，而不属于 Y 的单元格的值都为 0 。
可以证明，写出 Y 至少需要进行 3 次操作。

示例 2：

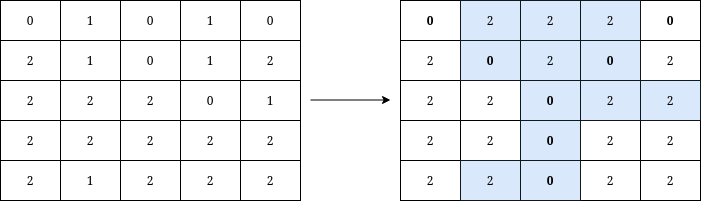
输入：grid = [[0,1,0,1,0],[2,1,0,1,2],[2,2,2,0,1],[2,2,2,2,2],[2,1,2,2,2]]
输出：12
解释：将在矩阵上写出字母 Y 需要执行的操作用蓝色高亮显示。操作后，所有属于 Y 的单元格（加粗显示）的值都为 0 ，而不属于 Y 的单元格的值都为 2 。
可以证明，写出 Y 至少需要进行 12 次操作。

提示：

• 3 <= n <= 49
• n == grid.length == grid[i].length
• 0 <= grid[i][j] <= 2
• n 为奇数。