现有一棵由 n 个节点组成的无向树，节点编号从 0 到 n - 1 ，共有 n - 1 条边。

给你一个二维整数数组 edges ，长度为 n - 1 ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条边。另给你一个整数数组 restricted 表示 受限 节点。

在不访问受限节点的前提下，返回你可以从节点 0 到达的 最多 节点数目。

注意，节点 0 不 会标记为受限节点。

 

示例 1：

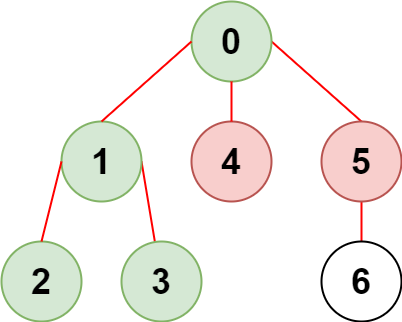
输入：n = 7, edges = [[0,1],[1,2],[3,1],[4,0],[0,5],[5,6]], restricted = [4,5]
输出：4
解释：上图所示正是这棵树。
在不访问受限节点的前提下，只有节点 [0,1,2,3] 可以从节点 0 到达。

示例 2：

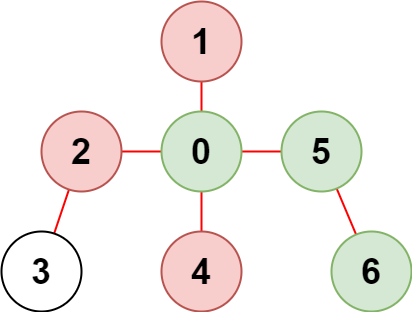
输入：n = 7, edges = [[0,1],[0,2],[0,5],[0,4],[3,2],[6,5]], restricted = [4,2,1]
输出：3
解释：上图所示正是这棵树。
在不访问受限节点的前提下，只有节点 [0,5,6] 可以从节点 0 到达。

 

提示：