You are given a 0-indexed m x n binary matrix matrix and an integer numSelect, which denotes the number of distinct columns you must select from matrix.
Let us consider s = {c1, c2, ...., cnumSelect} as the set of columns selected by you. A row row is covered by s if:
matrix[row][col] (0 <= col <= n - 1) where matrix[row][col] == 1, col is present in s or,row has a value of 1.You need to choose numSelect columns such that the number of rows that are covered is maximized.
Return the maximum number of rows that can be covered by a set of numSelect columns.
Example 1:
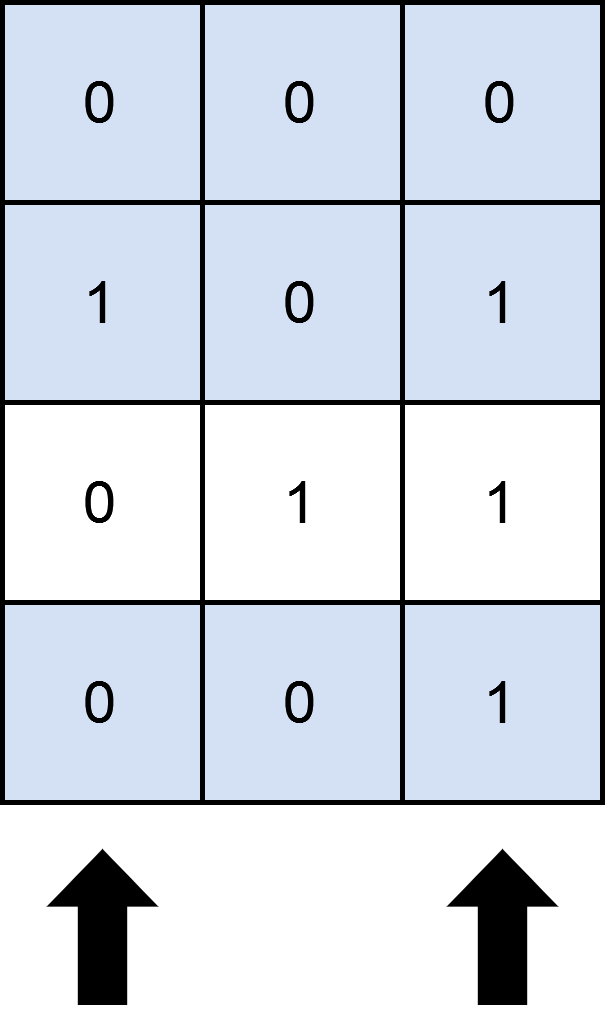
Input: matrix = [[0,0,0],[1,0,1],[0,1,1],[0,0,1]], numSelect = 2
Output: 3
Explanation: One possible way to cover 3 rows is shown in the diagram above.
We choose s = {0, 2}.
- Row 0 is covered because it has no occurrences of 1.
- Row 1 is covered because the columns with value 1, i.e. 0 and 2 are present in s.
- Row 2 is not covered because matrix[2][1] == 1 but 1 is not present in s.
- Row 3 is covered because matrix[2][2] == 1 and 2 is present in s.
Thus, we can cover three rows.
Note that s = {1, 2} will also cover 3 rows, but it can be shown that no more than three rows can be covered.
Example 2:

Input: matrix = [[1],[0]], numSelect = 1 Output: 2 Explanation: Selecting the only column will result in both rows being covered since the entire matrix is selected. Therefore, we return 2.
Constraints:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 12matrix[i][j] is either 0 or 1.1 <= numSelect <= n