游戏中存在两种角色:
给你一个下标从 0 开始的二维整数数组 statements ,大小为 n x n ,表示 n 个玩家对彼此角色的陈述。具体来说,statements[i][j] 可以是下述值之一:
0 表示 i 的陈述认为 j 是 坏人 。1 表示 i 的陈述认为 j 是 好人 。2 表示 i 没有对 j 作出陈述。另外,玩家不会对自己进行陈述。形式上,对所有 0 <= i < n ,都有 statements[i][i] = 2 。
根据这 n 个玩家的陈述,返回可以认为是 好人 的 最大 数目。
示例 1:
输入:statements = [[2,1,2],[1,2,2],[2,0,2]]
输出:2
解释:每个人都做一条陈述。
- 0 认为 1 是好人。
- 1 认为 0 是好人。
- 2 认为 1 是坏人。
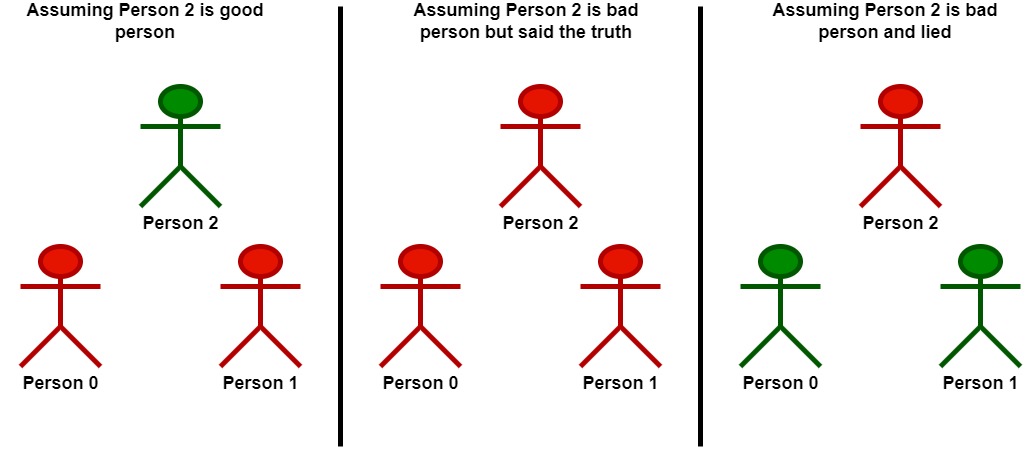
以 2 为突破点。
- 假设 2 是一个好人:
- 基于 2 的陈述,1 是坏人。
- 那么可以确认 1 是坏人,2 是好人。
- 基于 1 的陈述,由于 1 是坏人,那么他在陈述时可能:
- 说真话。在这种情况下会出现矛盾,所以假设无效。
- 说假话。在这种情况下,0 也是坏人并且在陈述时说假话。
- 在认为 2 是好人的情况下,这组玩家中只有一个好人。
- 假设 2 是一个坏人:
- 基于 2 的陈述,由于 2 是坏人,那么他在陈述时可能:
- 说真话。在这种情况下,0 和 1 都是坏人。
- 在认为 2 是坏人但说真话的情况下,这组玩家中没有一个好人。
- 说假话。在这种情况下,1 是好人。
- 由于 1 是好人,0 也是好人。
- 在认为 2 是坏人且说假话的情况下,这组玩家中有两个好人。
在最佳情况下,至多有两个好人,所以返回 2 。
注意,能得到此结论的方法不止一种。
示例 2:
输入:statements = [[2,0],[0,2]]
输出:1
解释:每个人都做一条陈述。
- 0 认为 1 是坏人。
- 1 认为 0 是坏人。
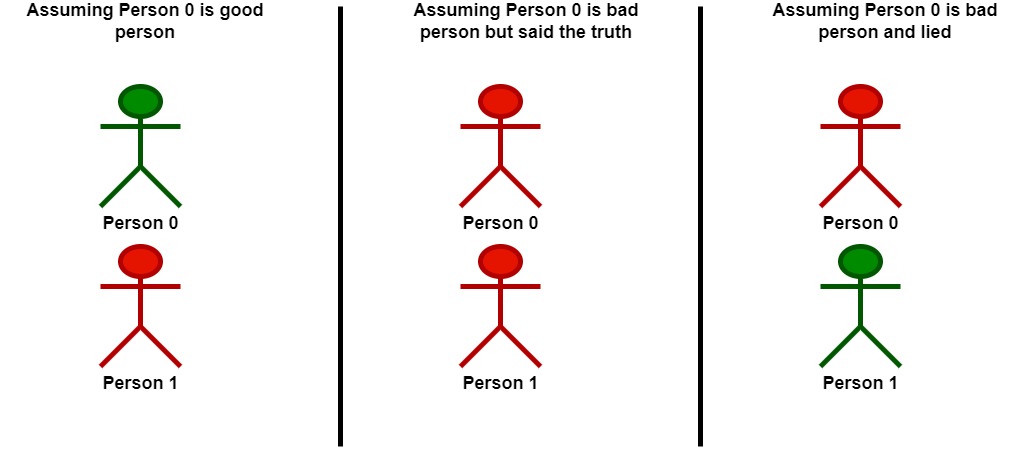
以 0 为突破点。
- 假设 0 是一个好人:
- 基于与 0 的陈述,1 是坏人并说假话。
- 在认为 0 是好人的情况下,这组玩家中只有一个好人。
- 假设 0 是一个坏人:
- 基于 0 的陈述,由于 0 是坏人,那么他在陈述时可能:
- 说真话。在这种情况下,0 和 1 都是坏人。
- 在认为 0 是坏人但说真话的情况下,这组玩家中没有一个好人。
- 说假话。在这种情况下,1 是好人。
- 在认为 0 是坏人且说假话的情况下,这组玩家中只有一个好人。
在最佳情况下,至多有一个好人,所以返回 1 。
注意,能得到此结论的方法不止一种。
提示:
n == statements.length == statements[i].length2 <= n <= 15statements[i][j] 的值为 0、1 或 2statements[i][i] == 2