城市用一个 双向连通 图表示,图中有 n 个节点,从 1 到 n 编号(包含 1 和 n)。图中的边用一个二维整数数组 edges 表示,其中每个 edges[i] = [ui, vi] 表示一条节点 ui 和节点 vi 之间的双向连通边。每组节点对由 最多一条 边连通,顶点不存在连接到自身的边。穿过任意一条边的时间是 time 分钟。
每个节点都有一个交通信号灯,每 change 分钟改变一次,从绿色变成红色,再由红色变成绿色,循环往复。所有信号灯都 同时 改变。你可以在 任何时候 进入某个节点,但是 只能 在节点 信号灯是绿色时 才能离开。如果信号灯是 绿色 ,你 不能 在节点等待,必须离开。
第二小的值 是 严格大于 最小值的所有值中最小的值。
[2, 3, 4] 中第二小的值是 3 ,而 [2, 2, 4] 中第二小的值是 4 。给你 n、edges、time 和 change ,返回从节点 1 到节点 n 需要的 第二短时间 。
注意:
1 和 n 。
示例 1:


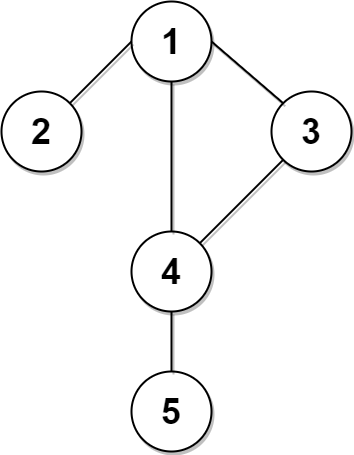
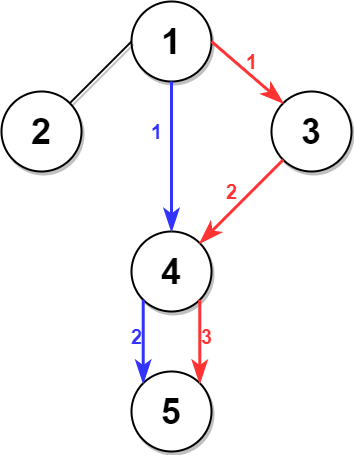
输入:n = 5, edges = [[1,2],[1,3],[1,4],[3,4],[4,5]], time = 3, change = 5 输出:13 解释: 上面的左图展现了给出的城市交通图。 右图中的蓝色路径是最短时间路径。 花费的时间是: - 从节点 1 开始,总花费时间=0 - 1 -> 4:3 分钟,总花费时间=3 - 4 -> 5:3 分钟,总花费时间=6 因此需要的最小时间是 6 分钟。 右图中的红色路径是第二短时间路径。 - 从节点 1 开始,总花费时间=0 - 1 -> 3:3 分钟,总花费时间=3 - 3 -> 4:3 分钟,总花费时间=6 - 在节点 4 等待 4 分钟,总花费时间=10 - 4 -> 5:3 分钟,总花费时间=13 因此第二短时间是 13 分钟。
示例 2:

输入:n = 2, edges = [[1,2]], time = 3, change = 2 输出:11 解释: 最短时间路径是 1 -> 2 ,总花费时间 = 3 分钟 第二短时间路径是 1 -> 2 -> 1 -> 2 ,总花费时间 = 11 分钟
提示:
2 <= n <= 104n - 1 <= edges.length <= min(2 * 104, n * (n - 1) / 2)edges[i].length == 21 <= ui, vi <= nui != vi1 <= time, change <= 103