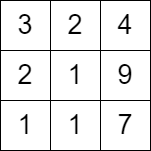
 输入:grid = [[3,2,4],[2,1,9],[1,1,7]]
输出:0
解释:从第一列的任一单元格开始都无法移动。
输入:grid = [[3,2,4],[2,1,9],[1,1,7]]
输出:0
解释:从第一列的任一单元格开始都无法移动。
给你一个下标从 0 开始、大小为 m x n 的矩阵 grid ,矩阵由若干 正 整数组成。
你可以从矩阵第一列中的 任一 单元格出发,按以下方式遍历 grid :
(row, col) 可以移动到 (row - 1, col + 1)、(row, col + 1) 和 (row + 1, col + 1) 三个单元格中任一满足值 严格 大于当前单元格的单元格。返回你在矩阵中能够 移动 的 最大 次数。
示例 1:
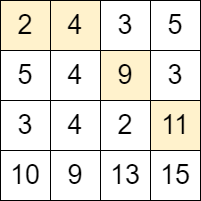
输入:grid = [[2,4,3,5],[5,4,9,3],[3,4,2,11],[10,9,13,15]] 输出:3 解释:可以从单元格 (0, 0) 开始并且按下面的路径移动: - (0, 0) -> (0, 1). - (0, 1) -> (1, 2). - (1, 2) -> (2, 3). 可以证明这是能够移动的最大次数。
示例 2:
输入:grid = [[3,2,4],[2,1,9],[1,1,7]] 输出:0 解释:从第一列的任一单元格开始都无法移动。
提示:
m == grid.lengthn == grid[i].length2 <= m, n <= 10004 <= m * n <= 1051 <= grid[i][j] <= 106